Solution-Solution of the nonhomogeneous differential

Solution of the nonhomogeneous differential equation

Assignment Help Mathematics

Reference no: EM13493237

In exercises 1-6, evaluate the integral.

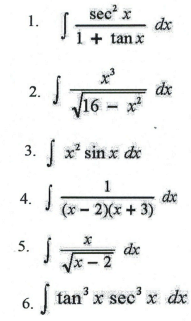
1846_Evaluate the integral.png

7. Determine whether the improper integral is convergent or divergent. If it converges, find it value.

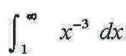
1055_Evaluate the integral1.png

8. Find the length of the curve, y = 2x^3/2, from x = 0 to x = 1

In exercises 9 and 10, determine whether the sequence converges or diverges. If it converges, find the limit.

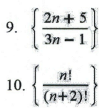
1557_Evaluate the integral2.png

In exercises 11-14, determine whether the series converges or diverges. Indicate the test(s) that you use to support your conclusion.

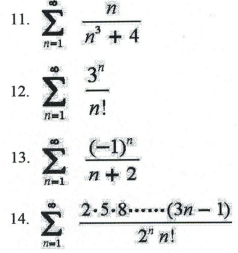
705_Evaluate the integral3.png

15. Find the values of x for which the series converges. Check endpoints.

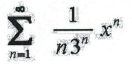
173_Evaluate the integral4.png

16. Find the first four terms of the Taylor series of f(x) = e^x at a = 1.

17. solve the differential equation.

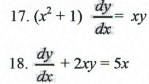
1780_Evaluate the integral5.png

19. Solve the initial-value problem.

y'' + 6y' + 9y = 0 , y(0) = 2 , y'(0) = 1

20. Find the general solution of the nonhomogeneous differential equation, y'' + 3y' - 10y = e^4x

Suggestion: use the method of undetermined coefficients.

Reference no: EM13493237

Questions Cloud

What must be the net torque that is acting on the wheel : A wheel has angular acceleration of 3.5 rad/s2 and an inertiaof 11.5 kg per m2. what must be the net torque that is acting on the wheel

Determine the angular velocity of the sphere : A solid sphere of mass m = 0.5 kg and radius r = 0.2 m, initially at rest, has a torque 9in units of N per m) applied to it about its CM. what is the angular velocity of the sphere

Determine the number of turns in the secondary : A transformer is to be used to provide power for a computer disk drive that needs 7.0 V (rms) instead of the 120 V (rms) from the wall outlet. Find the number of turns in the secondary

Explain redox reaction mno2 is oxidized to mno4 : For a particular redox reaction MnO2 is oxidized to MnO4- and Cu2 is reduced to Cu . Complete and balance the equation for this reaction in basic solution. Phases are optional.

Solution of the nonhomogeneous differential equation : Find the general solution of the nonhomogeneous differential equation and find the first four terms of the Taylor series of f(x) = ex at a = 1.

Explain substances is more likely to dissolve in liquid : Which of the following substances is more likely to dissolve in liquid CS2. a). Sodium Iodide b). Lithium Iodide c). Iodine d). Potassium iodide

What types of capital budgeting factors would you look : What types of capital budgeting factors would you look at when deciding whether to do this? What would be the relevant costs that you would consider in this decision?

What is the wavelength of this radiation : A diathermy machine, used in physiotherapy, generates electromagnetic radiation that gives the effect of "deep heat" when absorbed in tissue. What is the wavelength of this radiation

Find the capacitance of this capacitor : the dielectric strength, n, of a material is the largest electric filed it can be subjected to without breaking down, or in other words, What is the capacitance of this capacitor

User Account

All Pages

Solution of the nonhomogeneous differential equation

Reference no: EM13493237

Reference no: EM13493237

Questions Cloud

Reviews

Write a Review

Mathematics Questions & Answers

Questions on ferris wheel

Logistic map

Finding the probability of cards

Systems of ode

Derive the boolean expression

System of equations

Linear programming problem

Find the natural domain

Introduction to numerical methods

Chart of the topological manifold

Mathematics in computing

Complex problems

Assured A++ Grade

Academics

Major Subjects

Majors

Get In Touch

TERMS & POLICIES

HELP & SUPPORT