Reference no: EM13910
1. Prove directly from the axioms for a vector space that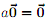 
for any scalar a.
Remark. Of course, this fact is not hard to believe when we think of the concrete examples of vector spaces that we've seen. The point is: is it true in any vector space, including examples we haven't seen or imagined yet?
2. Prove directly from the axioms for a vector space that if a~ v = ~ 0 for some scalar a, then either a = 0 or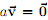 
.
HINT: Sometimes, when you need to show that something could not happen, a good way to argue is to suppose that it could and then arrive to a logical contradiction.
3. Determine if the following are subspaces of R2. Justify your answer. If a set is not a subspace, indicate what axiom is not satis?ed.
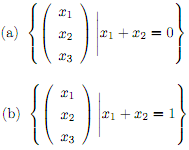
4. Let R44 be the vector space of all 44 matrices. Show that the set of skew-symmetric matrices
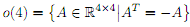
is a subspace of R.
Do you really need to write a typical 4 4 matrix A, then it's transpose, etc? Can you just use the properties of matrix arithmetics, transpose, etc.?
5. Determine if the following are subspaces of P3. Justify your answer. If a set is not a subspace, indicate what axiom is not satis?ed.
(a) The set of polynomials of degree 2
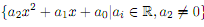
(b) The set of polynomials p(x) such that p(1) = 0.
(c) The set of polynomials p(x) such that p(1) = 1.
6. Prove that if U and V are subspaces of a vector space W, then their sum de?ned as
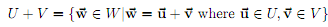
is also a subspace of W.