Reference no: EM13289726
Question 1:
Describe in words how you would go about calculating the work done by the electric field on the electron as it travels along its trajectory.
Consider a line of uniform charge Q that is bent into a 1-turn helix of radius R and height h. Suppose the helix is placed on an insulating surface and held such that the axis of the helix is vertical, as shown in the figure.
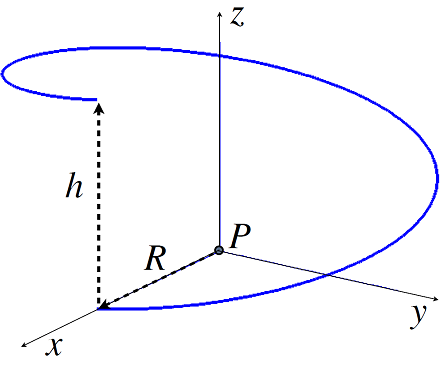
(a) Discuss how to calculate the electric field and potential generated by the helix. What are the main differences between calculating the electric field and the electric potential?
(b) Consider a point P that lies on the axis of the spiral where the axis intersects the horizontal surface. Show that the electric potential at point P is:
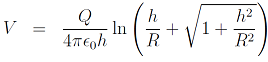
(c) To what simpler result does this expression approach in the limit that the height of the spiral goes to zero h -> 0? In your answer include a mathematical justification, and explain whether this is what you expect based on physical arguments.
Question 2:
A finite hollow insulating cylinder with radius a and length L and is shown. The cylinder is uniformly charged with a. positive surface charge density +'j.
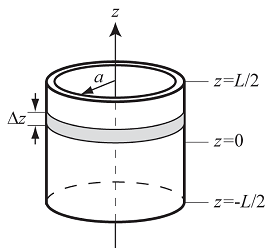
(a) Sketch a field line diagram of the electric field of the cylinder.
(b) Show that the z-comnonent of the electric field on the axis of the cylinder is
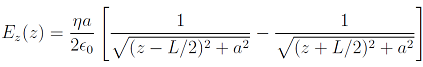
Hint: it may be useful to divide the cylinder into a. set of charged rings of thickness az (see diagram).
(c) What are the x- and y-components of the electric field on the axis of the cylinder? Give reasoning.
(d) Confirm that Ez (z) is equal to the electric field magnitude of a point charge in the limit z > {L, a}. Explain why you would expect this.
(e) Carefully graph the electric field magnitude Ez(z) as a function of z.
An electron is released from a point on the z-axis above the cylinder and constrained so it cannot move in the x or y directions. Describe in words how you would expect it to move.
(g) Describe in words how you would go about calculating the work done by the electric field on the electron as it travels along its trajectory