Reference no: EM133111060

MATLAB and Numerical methods

Problem: The formation of biodiesel through the methanolysis of triglycerides is of great interest due to its ability to produce renewable, environmentally friendly fuel from potentially waste materials. As a significant amount of research continues in the field, a vast literature is available concerning the kinetics of the process under different conditions and using different raw materials. A basic kinetic scheme isl,

MeOH +TG → BD + DG , k₁ = 0.4526 m³. kmo1^-1. day^-1

MeOH +DG → BD + MG, k₂= 0.3958 m³. kmol^-1. day^-1

Me0H + MG → BD +GL, k₃ = 0.3523 m³. kmol^-1.day^-1

In this reaction scheme, the reactant species methanol (MeOH) and triglyceride (TG) react to form biodiesel (BD) and glycerol (GL), along with diglyceride (DG) and monoglyceride (MG), which appear as intermediates.

If the reactions take place in a batch chemical reactor, assumed to operate isothermally, then the set of differential equations that describe the change in concentration of each of the chemical species is given by,

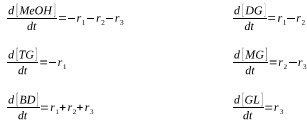
The respective reaction rates being:

r₁= k₁[Me0H][TG]; r₂= k₂ [MeOH] [DO; r₃=k₃[MeOH][MG].

If the initial concentrations of the reactant species are

[Me0H]=3kmol . m^-3 and [TG]=1kmoi.m^-3 (and the initial concentration of all other species is zero)

Objective: Your task is to solve this system of differential equations by hand using the Euler's method and in using both Simulink and MATLAB.

(a) Solve the first 2 time points, given a step size of 0.1, for each of the differential equations using the Euler's method calculation that you were shown you how to do by hand in Semester 1. These will need to be solved sequentially in the order presented in the table below (i.e. You will first need to solve [MeOH] @ t=0.1 and then go on to solve of [TG] @ t=0.1 etc.. Once you have completed this task you
should be able to complete the first 2 empty rows of the table below.

(b) Performing the hand calculations in part (a) should've demonstrated to you that for a complex linked system of differentials it quickly becomes inefficient to perform hand calculations. Develop a Simulink model to simulate the system of equations and plot the concentration of each species over time. You should use a Fixed-step Solver: odel (Euler); with a Fixed-step size 0.1.

(c) The final task is to write the MATLAB code to solve this problem using the odes45 function. This will require you to generate a script file and a function file containing the system of ODEs to pass to the ode45 function in you script (similar to the example in slide pack 5).

The required work, structure of the report and marking criteria are as follows,

Question 1. Provide Euler's hand calculations (typed) for the first 2 rows of the table. Any 2 example calculations will be sufficient to include in the report alongside the completed tables and will ensure unique reports.

Question 2. Use Simulink to solve the ODEs. Include the Simulink block diagram (signals labelled) in the main body of the report along with the output plot of the 6 species. Provide the 1st 10 and last 10 rows of the matrix of concentrations in a table.

Question 3. Develop the code to solve to problem an provide the annotated (commented) script and function file that you developed in the main body of the report along with the output plot of the 6 species. Provide the 1st 10 and last 10 rows of the matrix of concentrations in a table from the variable step size solver ode45.

Question 4. Provide 3 bullet points on your learning outcomes from this report. Marks will also be awarded in this section for presentation and layout of the report to a professional standard and ability to follow instructions.