Reference no: EM134521

Question 1

Let X; Y;Z denote i.i.d. random variables with Exp() distribution for λ > 0. Find P(X < Y + Z):

Question 2

Suppose that new international students arrive in London according to a Poisson process of rate λ = 2 per day.

1. Compute the expected time until the 100^th student arrives.

2. What is the probability that the time between the arrival of the 200th and the 201st student exceeds 2 days?

3. Do you think we are working with a reasonable model here? How could you improve this model?

Please state clearly any assumptions you might make.

Question 3

Simulation of a Poisson and a compound Poisson process:

1. Write down an algorithm which can be used to simulate a Poisson process N with rate  > 0 over the time interval [0; T] for a T > 0.

2. Now extend your algorithm to simulate a compound Poisson process with standard normally distributed jump sizes on the time interval [0; T].

Question 4

Let N denote an inhomogeneous Poisson process with intensity function λ(t) = t + exp(t) for t  0.

1. Find P(N2 N1 = 0).

2. Find P(N1:4 = 2;N2:3 = 3) and comment on your result.

Question 5

For each claim, state whether it is true or false.

1. The inter-arrival times of a Poisson process with rate  are independent and exponentially distributed with parameter .

2. The inter-arrival times of a compound Poisson process with rate  are independent and exponentially distributed with parameter .

3. The inter-arrival times of an inhomogeneous Poisson process with intensity function (t) are independent and exponentially distributed with parameter (t).

4. Let N denote a Poisson process with rate  > 0. Given that Nt = n for an n 2 N, the joint distribution of the jump times T1; : : : ; Tn equals the joint law of n independent uniform random variables on [0; t].

5. A Poisson process is a Markov chain in continuous time.

Question 6

Let

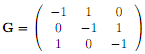
denote the generator of a continuous-time Markov chain. Find the stationary distribution.