Reference no: EM133043651

PDE4905 Engineering Simulation - Middlesex University London

Problem 1 Simple Linear Programming and Optimisation

A small factory has two products (A and B). In order to keep the factory running, at least 20+k units of products must be produced each day where k is the largest digit of your student number. Product A costs $200 to produce, while Product B costs $100 to produce. The total costs must be less than $8000 as the budget each day. In addition, the market regulations require that the number of Product B cannot exceed twice the number of Product A, but must be at least more than half the number of Product A.

If each Product A gives a profit of $40 and each Product B gives a profit of $60, design a simple daily production portfolio (in terms of the numbers of Products A and B to be produced) so that the total profit is maximized.

- Write this problem as a simple linear programming problem with the objective and all appropriate constraints.
- Find its optimal solution by solving it using two different methods (e.g., graphical method and Excel Solver/Matlab).

Problem 2 Transportation/Resource Allocation

A product has 4 suppliers (A, B, C, D) that produce a total of 1500 units. All the units produced should be distributed to 6 demand stations/customers (P, Q, R, S, T, W). The transportation costs for transporting one unit from a supplier to a station are given in the following table:

Thus, its transportation cost matrix is simply

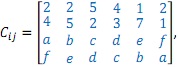
where a, b, c, d, e, and f are the single digits of your student number in the format "M00abcdef". For example, if your number is M00152379, you have a=1, b=5, c=2, d=3, e=7 and f=9.

Let xij be the integer quantities to be distributed from Suppliers (Si=A,B,C,D) to Demand stations (Dj=P,Q,...,W). The objective is to distribute the product such that

Minimize ∑_i=1⁴∑_j=1⁶ c_ij x_ij,

subject to various constraints.

• Write down the mathematical formulation for this problem with the objective and all relevant constraints and discuss their meaning briefly.
• Solve the problem using either Excel Solver or Matlab/Octave to find its optimal solution. Check if the solution can indeed satisfy all the constraints.

Problem 3 Supermarket Staff Scheduling

A busy supermarket is open 24 hours daily. It has a set of 20 checkout counters, though the actual number of checkouts needed ranges from 2 to 20, depending on the time of day. The number of staff needed to provide a satisfactory service varies at different hours as summarized in the following Table:

The supermarket employs 10 full-time staff and a large number of part-time staff. Part-time staff typically can work a 6-hour shift every day and can start on the hour between 9:00 am to 1:00 pm, or at 3:00 pm, 6:00 pm, 9:00 pm or 3:00 am.

Full-time staff work at most 40 hours per week between 9:00 am to 5:00 pm with a daily wage of £90 for 8 hours per day, while part-time workers are paid at a standard rate of £8 per hour (i.e., £48 per day for 6 hours). The company policy only permits that up to 80% of the total working hours of any day to be part-time hours.

The main Problem is to schedule the staff so that the total staff costs are minimized on a daily basis.

• Formulate the scheduling problem in terms of a linear programming problem with a correct objective and all appropriate constraints. Explain in detail why your mathematical formulation is appropriate, including any assumptions that you may have used.
• Solve your staff scheduling problem using either Excel Solver or Matlab (intlinprog)/Octave (glpk). Summarize your solution procedure (including screenshots if appropriate) and present the main results with a brief discussion.
• Check if all the required numbers of counters are met.

Problem 4

For this part, you can either choose the LP (Option 4A) or Simulink (Option 4B). You only need to choose one, no additional marks if you choose to do both.

Option 4A: Manufacturing Portfolio

A garden furniture company has 4 products: garden tables, garden chairs, garden benches, and parasols. A garden table takes 8 hours to produce with the material cost of £60. A garden chair takes 6 hours to make with the material cost of £20. A garden bench takes 4 hours to make with the material cost of £25. A parasol takes 2 hours to make with the material cost of £10. Each week, there are 800 hours available with a weekly budget of £3000 for material costs. To make maintain diversity of the products, the company will produce at least 5 units for each product.

A garden table typically comes with 4 chairs, whereas a bench may also have 4 chairs. Thus, the number of chairs should be at least 4 times the total number of tables and benches. Some customers may also wish to buy a parasol if they buy a table. Thus, the number of parasols should not exceed the number of tables.

The profits per unit are £260, £140, £60, and £50 for tables, benches, parasols, and chairs, respectively. The main objective is to organize the production portfolio so as to maximize the profit of the company on a weekly basis.

a) Formulate this problem as an LP with the objective and all the appropriate constraints.
b) Solve the LP and find the maximum profit and discuss your result.
c) The company seems to do well, so it decides to hire more people (thus more available hours) with the same material cost budget. If the number of available hours is now 1000, will it affect the production portfolio? Should the company recruit more people? Discuss and explain.
d) Another strategy is to increase the budget for raw materials to £5000 per week with the available hours unchanged. Will this strategy increase the profit? Discuss your findings.
e) The company later realizes that the garden benches do not sell well, so it may consider not to produce any benches at all. Will this potential change increase or decrease the profit (assuming that the other conditions remain the same)? Discuss and explain briefly.

Option 4B: Simulink Simulation

Check the Simulink model for a simple electric motor that you have built in class.

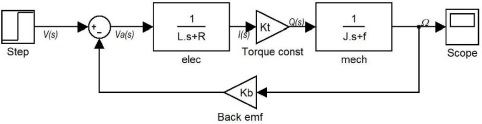
This model used the trident motor parameters with two different sets of parameters (please choose one):

Extend and/or reformulate the model to carry out the following scenarios:

• Use a single second-order transfer function

H(s) = K_t/((Ls + R)(Js + f)) = Kt/(LJs2 + (Lf + Rj)s + Rf)

to simulate the motor to see if you can obtain the same result using the same parameters.

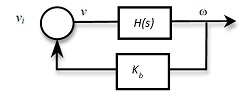
• By applying the voltage of Vnom=5 volts, a robotic arm attached to the motor should rotate θ = 100°, however, at t* = 5 seconds, the robotic arm is disturbed by a vibration that that takes the form

a(t) = θ₀ u(t - t*)e^{-(t - t*)}cos(Π(t - t*)) ,   θ₀ = -40°,

where u(t) is a Heaviside step function. This disturbance (also called perturbation) causes the robotic arm to bounce back 40 degrees at t* = 5. Implement this perturbed model in your Simulink model and display your results to show the perturbation.

Report and Guidelines

Write a report and explain your understanding of linear programming, Simulink and their applications with the following tasks:
1. Complete Problem 1
2. Complete Problem 2
3. Complete Problem 4
4. Complete Problem 4
Show your results with screenshots and/outputs when appropriate.

The report should include your models/formulations and the main results on a series of tasks. Your mathematical formulations and programs should be clearly presented, and an evaluation of your solutions can be discussed in the light of all assumptions made and if your solutions can indeed satisfy all the constraints.

Your report must be in the form of a standard technical report or article to include:

Title page: The first page with the title of your assignment, your full name and student number.

Abstract: About 100 words, no more than 150 words.

Introduction: Include a brief review of the background and literature, and explanations of linear programming, transport/resources allocation problems, etc., citing relevant references when appropriate.
Methods: Describe your modelling technique, the structure of your model or implementations. Justify your approaches to formulating the model and cite relevant references when appropriate.
Results: Present your main results and explain them in detail. Use graphs and/or tables when appropriate.

Discussion: Discuss your mathematical formulations, solutions to your problems/tasks and their implications for real-world systems, such as the staff scheduling for a large airline or a factory in real time.

Conclusions: Draw brief conclusions and evaluate any possible limitations.

Attachment:- Engineering Simulation.rar