Reference no: EM132235173

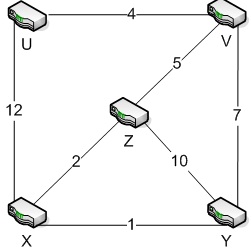
Question 1. Consider the network shown below, and assume that each node initially knows the costs to each of its neighbors. Consider the distance-vector algorithm and show the distance table entries at each node iteration by iteration until the algorithm converges at all nodes.

Question 2. Consider the network fragment shown below. Node x has only two attached neighbors, w and y. Node w has a minimum-cost path to destination u (not shown) of 5, and y has a minimum-cost path to u of 6. The complete paths from w and y to u (and between w and y) are not shown. All link costs in the network have strictly positive integer values (i.e. 1, 2, 3, ...).

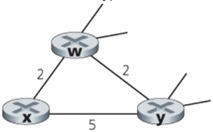
a. Give x's distance vector for destinations w, x, y, and u. Also, give distance vectors x receives from its neighbors w and y.

a. Give all valid link-cost changes for either c(x, w) or c(x, y) such that x will inform its neighbors of a new minimum-cost path to u as a result of executing the distance-vector algorithm.

b. Give all valid link-cost changes for either c(x, w) or c(x, y) such that x will not inform its neighbors of a new minimum-cost path to u as a result of executing the distance-vector algorithm.

c. Give all valid updates received by X (with regard to the cost of the least-cost to U, i.e. either Dw(U) or Dy(U)) such that X will inform its neighbors of new least-cost path to U as a result of executing the DV algorithm.

d. Give all valid updates received by X (with regard to the cost of the least-cost to U, i.e. either Dw(U) or Dy(U)) such that X will NOT inform its neighbors of new least-cost path to U as a result of executing the DV algorithm.

Attachment:- Assignment.rar