Reference no: EM13898896

1.  In 1676, the Danish astronomer Ole Roemer had one of those "oho" moments in science. He concluded from accumulated observations of eclipses of Jupiter's moon at different times of the year that light must travel at finite speed and needed 1300 s to cross the diameter of Earth's orbit around the Sun. Using 300,000,000 km for the diameter of Earth's orbit, calculate the speed of light based on Roemer's 1300-s estimate. How does it differ from a modern value for the speed of light?

2.  More than 200 years later, Albert A. Michelson sent a beam of light from a revolving mirror to a stationary mirror 15 km away. Show that the time interval between light leaving and returning CO the revolving mirror was 0.0001 s.

3.  The Sun is 1.50 X 10¹¹ m from Earth. How long does it take for the Sun's light to reach Earth? How long does it take light to cross the diameter of Earth's orbit? Compare this time with the time measured by Roemer in the 17th century (Problem 1).

4.  Show that it would take 2.5 s for a pulse of laser light to reach the Moon and to bounce back to Earth.

5.  The nearest star beyond the Sun is Alpha Centauri, 4.2 X 10¹⁶ m away. If we were to receive a radio message from this star today, show that it would have been sent 4.4 years ago.

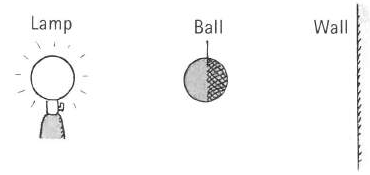
6.  A ball with the same diameter as a lightbulb is held halfway between the bulb and a wall, as shown in the sketch. Construct light rays (similar to those in Figure) and show that the diameter of the umbra on the wall is the same as the diameter of the ball and that the diameter of the penumbra is 3 times the diameter of the ball.

7. A certain radar installation tracks airplanes by transmitting electromagnetic radiation of wavelength 3 cm. (a) Show that the frequency of this radiation is 10 GHz. (b) Show that the time required for a pulse of radar waves CO reach an airplane 5 km away and return is 3.3 X 10^-5 s.

8. The wavelength of light changes as light goes from one medium to another, while the frequency remains the same. Is the wavelength longer or shorter in water than in air? Explain in terms of the equation speed = frequency X wavelength. A certain blue-green light has a wavelength of 600 nm (6 X 10^-7 m) in air. What is its wavelength in water, where light travels at 75% of its speed in air? In Plexiglas, where light travels at 67% of its speed in air?