Reference no: EM132590559

Math 260 Assignment -

Q1. a) Show that R² is an inner product space under the following definition of inner product.

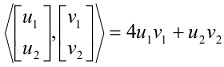
b) Let v^→ = (v₁, v₂, v₃) and u^→ = (u₁, u₂, u₃) and define an operation (u, v) = u₁v₁ + u₂ + u₃v₃. Determine if this operation is an inner product on R³, and if it is not, state which condition fail.

c) The trace of a square matrix A is denoted by tr(A) and is defined to be the sum of the entries on the main diagonal of A. Let A and B be elements of M_n(R). Show that (A, B) = tr(AB^T), defines an inner product on M_n(R).

Q2. Consider the polynomial space P_n[-1, 1] with the inner product (p, q) = _-1∫¹p(t)q(t)dt.

a) Show that every polynomial p ∈ P_n for which p(1) = p(-1) = 0 is orthogonal to its derivative.

b) Show that the subspace of polynomials in even powers (e.g. p(t) = t² - 5t⁶) is orthogonal to the subspace of polynomials in odd powers.

c) Let p₁(x) = 3x² - 1 and p₂(x) = 2x + 3. Determine

i. ||3p₁(x) - 2p₂(x)||;

ii. The angle theta between p₁(x) and p₂(x)

iii. proj_p2(x)p₁(x)

Q3. Let S = {s₁, s₂, . . . , s_n} be a set of vectors in an inner product vector space V. Prove that S^⊥ = {v ∈ V|< v, s_i >= 0 for i = 1,2, . . . n} is a subspace of V.

Q4. Find a basis for the rowspace(A) and colspace(A) where A =.

Q5. Prove/disprove if the following is a linear transformation.

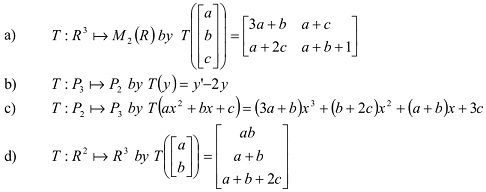
Q6. Find the kernel and range of the following linear transformation T, then determine whether T is injective, subjective or bijective.

a) T: V|→ V defined by T(v) = ½v, for ∀ v ∈ V.

b) T: R³|→ R² defined by T(x, y, z) = (x - y + 2z, y - x - 3z)

c) T is defined by.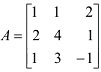

d) T: M₂(R)|→ P₂ defined by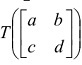= (3a + c + d)x² + (a + b+ 2d)x + 3c + 5d.

e) T: P₂|→ R³ defined by T(ax² + bx + c) =.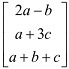

Q7. Let T: R²|→ R³ be a linear transformation defined by the matrix:. Give an example of a vector v^→ ≠ 0^→ such that v^→ ∈ Ker(T); v^→∈ Im(T).

Q8. Prove that the mapping T : R³|→ R³ defined by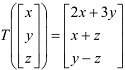is injective and surjective. Find its inverse.

Q9. Find the Eigenvalues and associated Eigenvectors for the following matrices:

Q10. i) Find all eigenvalues of A.

ii) For each eigenvalue, find as many linearly independent eigenvectors as possible.

iii) If A is diagonalizable, find a nonsingular matrix P and a diagonal matrix D such that D = P^-1AP.

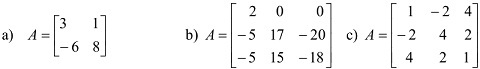
Q11. Let A and B be similar matrices: Prove the following:

a) If A is non - singular, then B is nonsingular.

b) If A is nonsingular then A^-1 and B^-1 are similar.

c) A^T and B^T are similar.

Q12. Find the Eigenvalues and associated Eigenvectors for the following matrices:

Q13. Given that the eigenvalues of 2 x 2 matrix A are 2 and -1 corresponding eigenvectors (1, 2)^T and (1, 3)^T, use the method of diagonalization to determine A⁴.

Q14. Let B = {cosx, sinx, x cosx, x sinx} and let V = span {B}, define T: V|→ V by T(f(x)) = d/dx f(x)

a) Find the matrix representation of T with respect to the basis B. [T]_B^B.

b) Find the rank and nullity of [T]_B^B.

c) Is [T]_B^B diagonalizable?