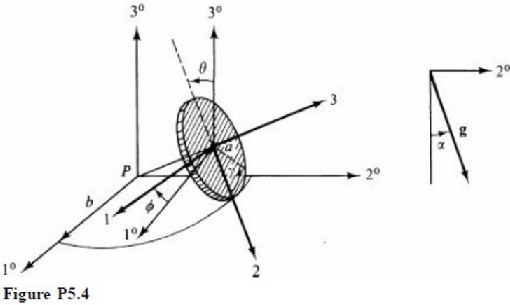
Reference no: EM13903393

(a) Show that in general the angular velocity of the rolling tack is given by

ω= Θe₁^{^} + Φ cosΘ e_^{^}2 + (ba^-1 - sinΘ)Φe^{^}₃

(b) Show that the kinetic energy of the tack is given by

T = 1/2 I₁Θ² + 1/2 I₁Φ² cos²Θ + (2a²)^-1 I₃(b-asinΘ)²Φ² + 1/2M(b-asinΘ)²Φ² + 1/2Ma²Θ²

(c) Show that the potential energy of the tack is given by

V= - Mg.R = -Mg[(b-asinΘ)sinαcosΦ - acosαcosΘ]

(d) Construct the lagrangian L(Φ,Θ;Φ,Θ) and write Lagrange's equations for Φ and Θ incorporating the constraint Θ =Θo= arcsin (a/b) with a Lagrange multiplier λΘ.

(e) Show that Φ satisfies the pendulum equation with angular frequency given by

Ω² = (9/a)( sinα 4 /acot ΘocosΘo6 + tan²Θo)

(f) Inteipret λo. For small oscillations of the pendulum, show that the condition that the thumbtack not tip over is simply

tanα< tan Θo