Reference no: EM13920671

1. If f is a continuous function in an interval D and if g is a continuous function in R, show that the composite g o f is continuous.

2. If f is a continuous function defined in an interval D, show that the restriction of f to a second internal contained in D is continuous.

3. If f is a continuous function defined in (a, b) and if lim_x→b f (x) = u, show that a continuous function g : [a, b] → R is defined by

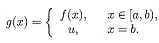
4. Suppose f is a continuous function in an interval D.

(a) Show that the function |f| defined by |f|(x) = |f(x)| is continuous.

(b) Show that the functions f₊ and f_- defined by

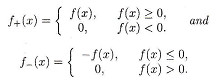
are continuous. (Hint: Consider 1/2(f +|f|).)

(c) Show that f = f₊ - f_-

Recall that a continuous function is a real-valued function whose value at a given point is the limit of the values at points approaching the given point. Continuous functions in a closed interval automatically satisfy a stronger condition.

Examples-

1. The infinite sequence 1,2,3,... of natural numbers. This sequence does not converge.

2. The infinite sequence 0,1, -1,2, -2,3,-3,... which lists all the integers. This sequence does not converge.

3. The infinite sequence (x_n)_{n ≥1} defined by x_n = 1/n. This sequence converges to 0.

4. The infinite sequence (x_n)_{n ≥1} defined inductively by x₁ = 1, and xn = _i=1Σ^n-12^xi. This sequence does not converge.

5. The infinite sequence (x_n)_{n ≥1}, defined by: x_n is the nth largest prime number. This sequence does not converge.

6. The infinite sequence (x_n)_{n ≥1}, defined by: x_n = 1+(-1/2)ⁿ. This sequence converges to 1.

Exercise - As always, provide complete proofs for your answers.

In each of the examples above supply proofs for the statements about convergence.