Reference no: EM13835556

Question 1: Consider the following sequential-move game between Ann and Bob.

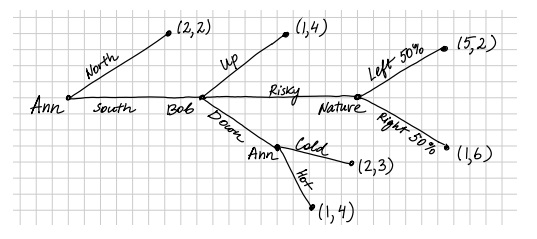
External uncertainty is handled by an outside player called "Nature". Nature chooses "Left" with probability 50% , "Right" with probability 50%.

A. The inclusion of a random event (a choice made by Nature) means that the players need to determine their expected payoffs when Nature moves. Calculate the players' expected payoffs in the situation where Ann chooses "South" and Bob chooses "Risky," giving rise to Nature's choice of "Left" or "Right".

B. Use backward induction to find all rollback equilibria.

C. How many strategies does each player have? For each player, list all his/her strategies.

Question 2: The Saga of Big Panda and Little Panda. Big Panda (BP) and Little Panda (LP) live on a deserted island in the South Pacific. Their food is the warifruit which grows only from the highest branches of the waritree. To get the fruit, one of the pandas
must climb all the way up the tree, creep out on the precarious branch and shake vigorously until the fruit drops.

Measurements show that a warifruit is worth 10 kilocalories (Kc) of energy. The cost to BP of climbing the tree is 2 Kc but is negligible (meaning 0 Kc) for LP. If both pandas climb the tree to get the fruit, BP takes most of the fruit and gets 7 Kc leaving LP only 3 Kc of fruit. If only LP climbs the tree, BP has eaten 9 Kc of the fruit by the time LP gets back down leaving him only 1 Kc. If BP climbs the tree, LP gets to eat 4 Kc of fruit before BP can climb down and get the other 6 Kc of fruit. If no pandas climb the tree, then they do not get
the fruit, and both get 0 Kc.

A. Assume the pandas decide simultaneously whether to climb the tree. Write down the payoff matrix for this game.

B. Find all Nash equilibria in pure strategies.

Question 3: Consider the same setting as in Question 2. Now assume that Big Panda gets to move first and that Little Panda observes this decision and then gets to choose.

A. Draw the game tree for this game.

B. Find the rollback equilibrium. What is the equilibrium outcome?

Question 4: Which of the following quotes could have been spoken by a player after a game in which every player acted in a way that was consistent with the definition of a Nash equilibrium? Explain. You can give an example to justify your answer.

1. "I am really annoyed. I could have been much better off. If only I'd known that you'd do ‘that', I would have done ‘this' instead of what I did."

2. "I am really annoyed. All of us players could have been much better off if only we'd cooperated with each other."

(a) quote 1

(b) quote 2

(c) both

(d) neither

Question 5: When a player has a dominant strategy in a simultaneous-move game, we can say that if he uses that strategy, then (given whatever actions his opponent has taken) his payoff at the end of the game is certainly higher than.

(a) his opponent's payoff

(b) the payoff he would have earned if he used a different strategy

(c) any other payoff that is possibly available to him in the game

(d) both (b) and (c) are correct

(e) all of (a), (b) and (c) are correct

Question 6: Consider the following zero-sum game:

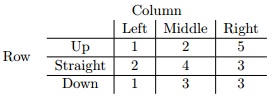
A. Does Row player have a strictly dominant strategy? A strictly dominated strategy?

B. Does Column player have a strictly dominant strategy? A strictly dominated strategy?

C. Use the method of iterated elimination of strictly dominated strategies to find the Nash equilibrium/ equilibria. Give the order in which the elimination occur.

D. Use the minimax method to find the Nash equilibrium/ equilibria. Did you get the same answer as in C?