Reference no: EM131092
Problem 1: As you know, utility functions incorporate a decision maker's attitude towards risk. Let's consider that the subsequent utilities were assessed for Stephanie Parker.
|
x
|
u(x)
|
|
-$400
|
0
|
|
-$365
|
10
|
|
-$320
|
20
|
|
-$270
|
30
|
|
-$200
|
40
|
|
-$110
|
50
|
|
$0
|
60
|
|
$130
|
70
|
|
$300
|
80
|
|
$600
|
90
|
|
$800
|
95
|
|
$1,100
|
100
|
Use these utilities to answer the following questions.
a) What is the monetary certainty equivalent for the following gamble: gain $130 with probability 0.4, lose $320 with probability 0.6.
b) What is the risk premium in a)? Illustrate the concept of a risk premium in addition to calculating its value for a).
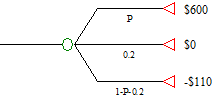
c) What probability P could make Stephanie become indifferent between getting $130 for sure or taking the following gamble?
Problem 2
a) The marketing department of a vitamin water company wishes to evaluate the maximum expected payoff from introducing a new strawberry drink. What decision, in terms of choosing the best investment level, could the marketing department make using the payoff table below? Consider that the probability that the market share is less than 1% is 0.2, that the probability that market share is between 1 and 4% is 0.5, and that the probability that market share is at least 4% is 0.3. Consider that the marketing department is risk neutral.
|
|
Market Share
|
|
Investment Level
|
< 1%
|
1%-4%
|
³ 4%
|
|
Low
|
300,000
|
400,000
|
500,000
|
|
High
|
-400,000
|
300,000
|
3,000,000
|
b) What is the maximum amount of money the company could spend to get more information about the market share?
Problem 3
Here is a basic risky decision problem:
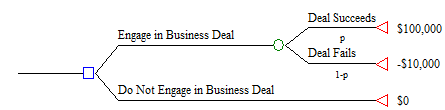
Using the template below, sketch the results of a sensitivity analysis on P(Deal Succeeds) for a risk-neutral decision maker. How high does P(Deal Succeeds) have to before before the decision maker could engage in the business deal?