SEHS4612 Numerical Methods for Engineers Assignment

Assignment Help Mechanical Engineering

Reference no: EM132501172

SEHS4612 Numerical Methods for Engineers Assignment - School of Professional Education and Executive Development - The Hong Kong Polytechnic University, Hong Kong

Question 1 - Consider the mass-spring system in the following figure.

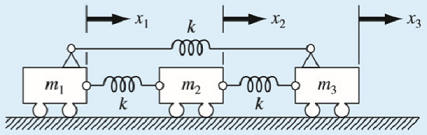
The frequencies for the mass vibrations can be determined by solving for the eigenvalues and by applying Mx¨ + kx = 0, which yields

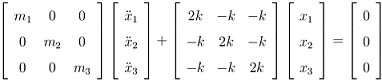
Applying the guess x = x₀e^iωt as a solution, we get the following matrix:

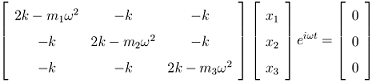
Assume m₁ = m₂ = m₃ = 1 kg, and k = 2 N/m and let

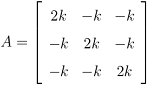
(a) Use the Power method with initial guess v₀ = to solve the dominant eigenvalue and the corresponding eigenvector of matrix A.

(b) Use the dominant eigenvalue to solve for the frequency (ω).

Question 2 - The following data for the density of nitrogen gas versus temperature come from a table that was measured with high precision.

T, K	200	250	300	350	400	450
Density, kg/m³	1.708	1.367	1.139	0.967	0.854	0.759

(a) Use Newton's interpolating polynomials of order 1 through 3 to estimate the density at a temperature of 330 K. Choose the sequence of the points for your estimates to attain the best possible accuracy. That is, the points should be centered around and as close as possible to the unknown. What is your best estimate?

(b) Repeat part (a) using the Lagrange polynomial of order 1 through 3.

Question 3 - Given the following set of data

x	2	2.2	2.4	2.6	2.8	3
y	1.00	1.07	1.13	1.18	1.23	1.27

It is known that the data can be described closely by the model

1/y = (1/a)e^b/ax

(a) Use least-squares linear regression to find a and b by applying appropriate transformations.

(b) Compute the coefficient of determination of the model in part (a).

Question 4 - It is known that the function f (x) passes through the following three points:

(1.8, 10.89), (2.0, 14.78), (2.2, 19.86).

Use forward and backward difference approximations of O(h), and centred difference approximation of O(h²) to estimate the first derivative of f(x) at x = 2.0. If the true value of f (2.0) = 22.17, find the absolute error for each approximation. How will it affect the error for each case if the step size h changes from 0.2 to 0.1?

Question 5 - Consider the integral

I = ₀∫¹f(x)dx = ₀∫¹1/(1+x²)dx = π/4

(a) Apply the trapezoidal rule to approximate I on three data points f (0), f (0.5), f (1.0).

(b) Estimate the error if the trapezoidal rule are used on nine equally spaced data points.

(c) If trapezoidal rule is used to approximate I to the accuracy of at least 10^-7, how many divisions, n, should be used for the approximation?

Reference no: EM132501172

Questions Cloud

Determining the cost of preferred stock-including flotation : Travis Industries plans to issue perpetual preferred stock with an $11.00 dividend. The stock is currently selling for $94.00, but flotation costs

How do find the predetermined overhead rate for the year : How do find the predetermined overhead rate for the year; at the beginning of the year, the total estimated manufacturing overhead

Cost of new equity-banyan co : The growth rate is a constant 8%, and the company has an expected dividend yield of 3%. The expected long-run dividend payout ratio is 20%, and the expected ret

Determine manufacturing overhead will have been : Tools for factory equipment $2,000 If actual direct labor costs for the year were $19,000, manufacturing overhead will have been

SEHS4612 Numerical Methods for Engineers Assignment : SEHS4612 Numerical Methods for Engineers Assignment Help and Solution - The Hong Kong Polytechnic University, Hong Kong. Solve the dominant eigenvalue

Effects of interest rates on future direction : If an analyst was considering the effects of interest rates on future direction of the economy, would she focus on the short rates as controlled by the central

What is evanec cost of retained earnings : What is Evanec's cost of retained earnings, rs? Do not round intermediate calculations. Round your answer to two decimal places.

What the standard hours allowed for decembers production is : What The standard hours allowed for Decembers production is? The Fischer Corporation uses a standard costing system data have been assembled for December

What is pearson cost of common equity : What is Pearson's cost of common equity? Do not round intermediate calculations. Round your answer to two decimal places.

User Account

All Pages