Reference no: EM1380603

Q1

In the second order differential equation we described the motion of the pendulum. Unfortunately, the differential equation is nonlinear, so at that time, we linearized about ??=0 which means that the solution will be good only for small angles. Recall that the differential equation is

                                  d²??/dt² + c/mL d??/dt + g/L sin(??) = 0

For our project, we will let m=1, L=1, c=0.5andrecallg=9.8.Therefore, our differential equations

                                                          d²??/dt² + 0.5d??/dt +9.8 sin(??) = 0

1) Show the steps in using the change of variables

x = ??

y = ??'

 

to convert the above nonlinear, second order differential equation (the one with numbers) to the first order system  dx/dt = y dy/dt = -9.8sin(x) - 0.5y

Q2

Use NumSysDE.xmcd to numerically solve the differential equation with the

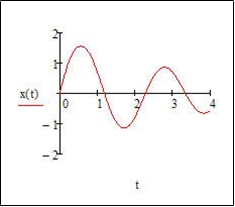
initial conditions ??(0)=0and??'(0)=5(i.e.x(0)=0 and y(0)=5) and then created the graph of ??vs t (keep in mind that x=??).

Use this graph to discuss the actual motion of the pendulum in the time interval 0≤t≤4. That is, where is the pendulum at time t=0? Then as time increases, is the pendulum moving clock wise or counter clock wise and for approximately how long? ETC.

Q3

Use NumSysDE.xmcd to numerically solve the differential equation with the given initial conditions and then created the graphs of x vs tin each case (keep in mind that x=??).

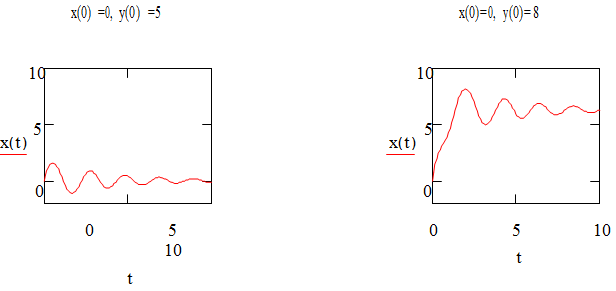
Using the graphs to think about the actual motion of the pendulum, explain why the graphs appear as they do. In particular, you should be able to explain why limx(t)_t→∞= 2π in the second graph.

Q4.

a) Verify that (0,0), (π, 0), and (2π, 0) are all critical points of the first order system (indeed, all(nπ,0) will be critical points).

b) Linearize the nonlinear system about the critical point (0,0) and determine stability. This means to actually write down the linearized system about (0,0) (so you will need to find partial derivatives and evaluate at x=0 and y=0),and then use the eigen values of the coefficient matrix to determine stability.

c) Linearize the nonlinear system about the critical point (π,0) and determine stability. This means to actually write down the linearized system about (π,0) (so you will need to find partial derivatives and evaluate at x=π and y=0), and then use the eigen values of the coefficient matrix to determine stability.

d) Linearize the nonlinear system about the critical point(2π, 0) and determine stability. This means to actually write down the linearized system about(2π,0) (so you will need to find partial derivatives and evaluate at x=2π and y=0),and then use the eigenvalues of the c