Reference no: EM133043004

Unit 28 Further Mathematics for Construction - Higher National Certificate/Diploma in Construction and the Built Environment

Assignment - Further Maths

Case Scenario:

You are working as an Engineering Research Technician in a research and development laboratory where good analytical skills and understanding of mathematics is essential for everyday work. Your line manager has informed you that you need to improve and update your present Mathematical skills to work effectively & contribute to the research team. The essential skills include Number theory, Matrices, graphical and numerical methods, Models of engineering systems using ordinary differential equations .

To test your suitability for this position in research, the following tasks have been compiled for you to complete.

Learning Outcome 1: Apply instances of number theory in practical construction situations.

Problem Task 1
a. Convert each number into denary,

• 11001.01

• 4D

b. calculate the following in both binary and denary

•11001+1001

Problem Task 2

Apply de'Moivre's theorem or otherwise to solve for Zo and C from these expressions given below :
Z0=Z/Y and C=Z*Y
Where:
• Z is a complex number.
• Y is also a complex number.
• Re (Z0) >0 and Re (C) >0
Find Z0 and C when:
Z = 1 + 5 j,Y = 1 - 3 j

Problem Task 3

a. Simplify the following equation:
G = 1 x e j^2Π x 2 x e^j0.5 x 0.5x e ^j0.75

b. Express the following expression in complex exponential form:

v=20sin (1000t-30°)

Problem Task 4

Find a formula for cos (3θ) in terms of cos (θ) and sin (θ) using de Moivre's Theorem.

Learning Outcome 2: Solve systems of linear equations relevant to construction applications using matrix methods

Problem Task 1

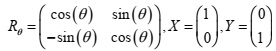
a) Determine the vector Z when θ = Π/2, Z = R_θ x ( X - Y )

b) Determine the determinant of the matrix R_θ when θ = Π/4

c) Determine the inverse of R_θ When θ = Π/4

d) Solve the following equation for

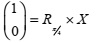
Problem Task 2

You have been asked by the structural engineering department to find the determinant and inverse of the following matrix

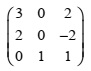
Problem Task 4
You have been asked to the following set of equations that have been obtained from the structural engineering Department and verify your calculations using computer methods
2x₂ + x₃ = -8
x₁ - 2x₂ - x₃ = 0
- x₁ + x₂ + 2x₃ = 3

Learning Outcome 3: Approximate solutions of contextualised examples with graphical and numerical methods

Assignment Brief and Guidance

Problem Task 1
The engineering department has developed the following equation for the bending moment of a beam and you have asked to investigate its behaviour
M ( x) = x³ - 3x² - 4
The Beam is 4m long and the design team suspect the is problem if the bending moment is zero in the range between 3-4m and you have been asked to
a) Plot the bending moment at 0.5m interval for the range 0 ≤ x ≤ 4m 0 ≤ x ≤ 4 and determine if the bending moment is zero in range 3m ≤ x ≤ 4m
b) Use the graph to estimate where the bending moment is zero
c) Use the bisection method to numerically estimate the exact location where the bending moment is zero
d) Newton-Raphson method to obtain the required location
e) Compare the results of the above method to determine which gives a best solution

Problem Task 2
The following offsets are taken from a chain line to an irregular boundary towards right side of the chain line.

chainage          0         25     50     75     100      125      150

Offset 'm'       3.6       5.0       6.5       5.5       7.3       6.0       4.0

Common distance d =25m
You have been asked to estimate the area using the following methods and compare and comment on their difference and accuracy.
a) Trapezium Rule
b) Simpson's Rule

Problem Task 3
The equation governing a body travelling in a water channel is given by the following equation

dv/dt = 1 - v²

Plot the velocity time graph for the object and determine the final velocity and the time taken to reach this velocity

Learning Outcome 4: Review models of construction systems using ordinary differential equations

Assignment Brief and Guidance

Problem Task 1

The equation of catenary is given by the following second order differential equation

y" = 5
x = 0, y = 100
x = 100, y = 100

Solve the above differential equation and plot the curve at 10m intervals.

Problem Task 2
The differential equation governing the motion of a particle is given by the following differential equation

y'' + 5 y = 0
t = 0, y = 20
Solve the above and plot the results and determine the amplitude and frequency of the oscillations

Problem Task 3
A new series of tests is carried out and the equation modified to
y ''+ 2 y + 5 = 0
y = 20, t = 0

Use Laplace transforms or any other method to solve the new equations and plot the function and comment on the results.

Assessment Criteria

LO1 Apply instances of number theory in practical construction situations.
P1 Apply addition and multiplication methods to numbers that are expressed in different base systems.
P2 Solve engineering problems using complex number theory.
P3 Perform arithmetic operations using the polar and exponential form of complex numbers.
M1 Deduce solutions of problems using de Moivre's Theorem.
D1 Test the correctness of a trigonometric identity using de Moivre's Theorem.

LO2 Solve systems of linear equations relevant to construction applications using matrix methods
P4 Ascertain the determinant of a 3x3 matrix.
P5 Solve a system of three linear equations using Gaussian elimination.
M2 Determine solutions to a set of linear equations using the inverse matrix method.
D2 Validate all analytical matrix solutions using appropriate computer software.

LO3 Approximate solutions of contextualised examples with graphical and numerical methods
P6 Estimate solutions of sketched functions using a graphical estimation method.
P7 Identify the roots of an equation using two different iterative techniques.
P8 Determine the numerical integral of construction functions using two different methods.
M3 Solve construction problems and formulate mathematical models using first-order differential equations.
D3 Critique the use of numerical estimation methods, commenting on their applicability and the accuracy of the methods.

LO4 Review models of construction systems using ordinary differential equations
P9 Determine first-order differential equations using analytical methods.
P10 Determine second- order homogeneous and non-homogenous differential equations using analytical methods.
P11 Calculate solutions to linear ordinary differential equations using Laplace transforms.
M4 Evaluate how different models of construction systems use first-order differential equations to solve structural or environmental problems.
D4 Evaluate first- and second-order differential equations when generating the solutions to construction situations.

Attachment:- Further Mathematics for Construction.rar