Reference no: EM133428

QUESTION 1

The research process can be concise in a sequence of steps which defines a orderly procedure for the objectives of a research to be met. Explain the sequence of steps involved.

QUESTION 2

The "School Compost Project" was launched in 2005 in minor schools in Mauritius with the purpose of developing an alertness of how to make use of biodegradable waste in a profitable way. Put in plain words how you would select a sample of secondary school students in Mauritius for the reason of eliciting their views on the "School Compost Project" by

(i) Simple random sampling,

(ii) Systematic sampling,

(iii) Cluster sampling.

Detailed the statistical efficiency of each of the sampling procedures.

QUESTION 3:

Survey researchers must stick to ethical principles when conducting surveys. The researcher has everyday jobs to at least the subsequent four categories of people:

- The Public

- Client/Sponsors

- The Profession

- Respondents

Endow with a short note on each of the category, which outlines the responsibility of the researcher.

QUESTION 4

When conducting an assessment there are many practical issues that need to be built into any proposal or plan. These subjects will affect the type of survey you end up conducting. record any four questions that help to help out with covering the practical side of survey design.

QUESTION 5

a) (i) Under what situation should you use the t-distribution in testing a hypothesis about a population mean?

(ii) If you test a hypothesis and refuse the null hypothesis in favour of the alternative hypothesis, does your test verify that the alternative hypothesis is correct? Explain.

B) A producer of cereal wants to test the performance of one of its filling machines. The machine is designed to free a mean amount of μ = 12 ounces per box and the manufacturer wants to detect any departure from this setting. This superiority study calls for randomly sampling 100 boxes from today's production run and determining whether the mean fill for the run is 12 ounces per box.

(i) Set up a test of suggestion for this study, using a level of significance α = 0.01. Give explanation of your working fully.

(ii) Suppose the sample yields the following results: 85.11=x ounces 5.0=s ounce

Use these data to conduct the test of hypothesis. Hence clearly explain your results in relation with the presentation of the filling machines.

QUESTION 6

A.) Make clear distinction between an interval estimator and a point estimator for a population mean.

B.) Some quality control experiments require destructive sampling (i.e. the test to determine whether the item is defective destroys the item) in order to measure some meticulous characteristic of the product. The cost of negative sampling often dictates small samples. For instance, suppose a manufacturer of printers for personal computers wishes to estimate the mean number of characters printed before the print-head fails. Presume the printer manufacturer tests 15 randomly selected print-heads and records the number of characters printed until failure. The table underneath provides the recorded data:

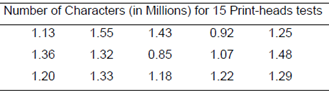
(i) Form a 99% confidence interval for the mean number of characters printed before the print-head fails. Interpret the result.

(ii) What assumption is required for the interval in part (i), to be valid? Is it reasonably satisfied?

A food-products company conducted a market study by randomly sampling and interviewing 1000 consumers to determine which brand of breakfast cereal they prefer. Assume 313 consumers were found to prefer the company's brand. Describe clearly, how would you estimate the true fraction of all consumers who prefer the company's cereal brand?

QUESTION 7

Individuals who report apparent wrongdoing of a corporation or public agency are known as whistle blowers. Two researchers developed an index to measure the extent of retaliation against a whistle blower. The index was based on the number of forms of reprisal actually experienced, the number of forms reprisal threatened and the number of people within the organization (e.g. co-workers or immediate supervisor) who retaliated against them. The table below lists the retaliation index (higher numbers indicate more extensive retaliation) and salary for a sample of 15 whistle blowers from federal agencies.

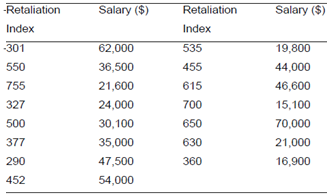
(i) Build a scatter plot for the data. Does it appear that the extent of retaliation increases, decreases or stays the same with an increase in salary? Explicate

(ii) Use the method of least squares to fit a straight line to the data.

(iii) Grid the least squares line on your scatter diagram. Does the least squares line support your answer to the question in part(a)? Explain.

(iv) Construe the y-intercept,β?^, of the least squares line in terms of this application. Is the interpretation meaningful? 0ˆβ

(v) Interpret the slope,β?1 , of the least squares line in terms of this application. Over what range of
is this interpretation meaningful? 1ˆβx