Reference no: EM13816676
Problem 1:
Consider the following game:
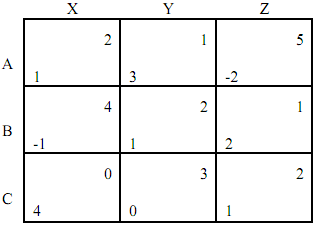
(a) Suppose that the Column player announces that he will play X with probability 0.5 and Y with probability 0.5 i.e., 1/2X ⊕ 1/2Y.
Identify all best response strategies of the Row player, i.e., BR(1/2 X ⊕ 1/2 Y) ?
(b) Identify all best response strategies of the Column player to Row playing 1/2 A ⊕ 1/2 B, i.e. BR(1/2 A ⊕ 1/2 B)?
(c) What is BR(1/5 X ⊕ 1/5 Y ⊕ 3/5 Z)?
(d) What is BR(1/5 A ⊕ 1/5 B⊕ 3/5 C)?
Problem 2: Here comes the Two-Finger Morra game again:
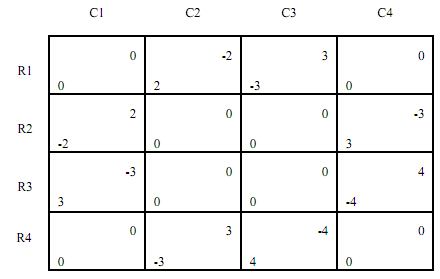
To exercise notation and concepts involved in calculating payoffs to mixed strategies, calculate the following (uR, uC stand for the payoffs to Row and Column respectively):
(a) uR(0.4 R1 ⊕ 0.6 R2, C2) =
(b) uC(0.4 C1 ⊕ 0.6 C2, R3) =
(c) uR(0.3 R2 ⊕ 0.7 R3, 0.2 C1 ⊕ 0.3 C2 ⊕ 0.5 C4 ) =
(d) u (0.7 C2 ⊕ 0.3 C4, 0.7 R1 ⊕ 0.2 R2 ⊕ 0.1 R3) =
Problem 3:
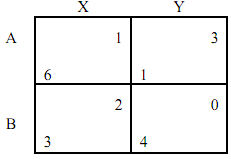
For the game above:
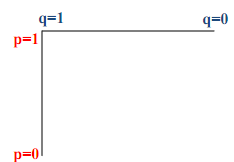
(1) Draw the best response function for each player using the coordinate system below. Mark Nash equilibria on the diagram.
(2) List the pair of mixed strategies in Nash equilibrium.
(3) Calculate each player's payoffs in Nash equilibrium.
Problem 4:
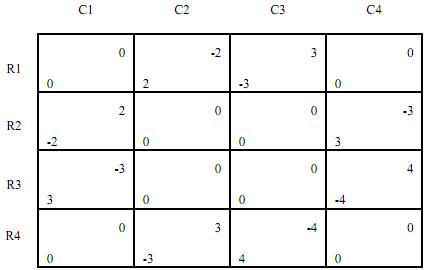
In the Two-Finger morra game above suppose Row decided to play a mix of R1 and R2 and Column decided to play a mix of C1 and C3. In other words, assume that the original 4 x 4 game is reduced to the 2 x 2 game with R1 and R2 and C1 and C3. Using our customary coordinate system:
(a) Draw the best response functions of both players in the coordinate system as above.
(b) List all Nash equilibria in the game.
(c) Calculate each player's payoff in Nash equilibrium.
Problem 5:
Lucy offers to play the following game with Charlie: "let us show pennies to each other, each choosing either heads or tails. If we both show heads, I pay you $3. If we both show tails, I pay you $1. If the two don't match, you pay me $x." For what values of x is it profitable for Charlie to play this game?
Problem 6:
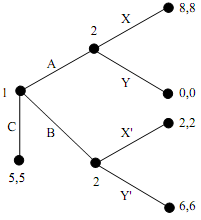
(a) Represent this game in normal form (payoff matrix).
(b) Identify all pure strategy Nash equilibria. Which equilibrium is the subgame perfect Nash equilibrium?
Important: In game theory people often use the same name to identify actions in different information nodes. This is the case above. In extensive form games, however, these actions are formally and conceptually different. You need to keep this distinction in mind when solving this problem. An easy way not to make a mistake is by using your own naming convention, e.g., X and X'.
-----------------------------
Problem 7:
Represent the following game in normal form and find its Nash equilibria.
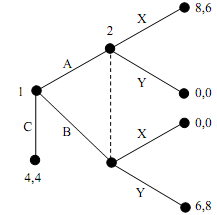
|
Does the partisan balance of congress matter
: Explain 3-4 strategies that you would implement to persuade one of the official players (you choose) to go along with you on deficit-reduction measures. Remember that you want to practice bipartisan and bicameral negotiations.
|
|
Formulate the conversation of employee
: Formulate the conversation you would have with the employee, based the concepts in your textbook. Summarize the conversation you would have with the employee's male co-worker, based on the concepts of your textbook.
|
|
Describe the event and explain what you did about it
: Recall an occasion when you experienced cognitive dissonance about a purchase. Describe the event, and explain what you did about it
|
|
Determine a multiple regression equation
: What are the various ways to determine what variables should be included in a multiple regression equation. Compare and contrast the following processes: forward selection, backward elimination, and stepwise selection.
|
|
Represent game in normal form and find its nash equilibria
: Represent the game in normal form and find its Nash equilibria - Draw the best response function for each player using the coordinate system below. Mark Nash equilibria on the diagram.
|
|
Measure the effectiveness of the advertising message
: Create a 2-3 minute video and show how you would determine the fundamental manner in which you will measure the effectiveness of the advertising message and how it aligns with corporate branding strategy
|
|
Concept of disintermediation
: Disintermediation is the elimination of intermediaries from a marketing channel. Research more on the concept of disintermediation and in a one to two-page paper explain: How can disintermediation be a benefit to businesses and consumers both
|
|
Define the financial statements to evaluate the performance
: Ratio analysis involves calculations that use the data from the financial statements to evaluate the performance of companies in different key areas. How would this information be used by a credit analyst as compared to someone is going to make a..
|
|
Specific type of organization
: For the purpose of this assignment, it helps to have a specific type of organization in mind. Provide an opening paragraph stating the nature of the company you are choosing for this assignment (e.g., retail organization, factory, school, police d..
|