Reference no: EM13376166

Question 1:

Figure 1 shows a large crawler crane in operation in a construction site

Figure 1   Crawler crane

a.Sketch a 2D pin-jointed structure model of the crane. You are allowed to make simplifications on the structure of the crane as you can not be expected to figure out all the structural details from the photograph. You do not need to model the individual braces in the jib structure.

b.Indicate on your sketch the type of forces (e.g. tension or compression) that each member is subjected to when the crane is carrying a load.

c.Apply a statical determinacy test on your model. If it is not a determinate system, discuss what alterations can be done to make it statically determinate.

Question 2

a-Explain briefly why this structure in figure 2 can be modelled as a pin-jointed structure (PJS) for the purpose of determining the axial forces in the members.

b. Show that the structure is statically determinate.

c. Determine the reaction forces at supports A and I.

d. Determine the axial force in member DF by using:

i. Method of sections

ii. Method of joints

You must show and clearly explain your working using appropriate free-body diagrams

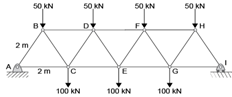
Figure 2   Truss structure (all members are of equal length)

Question 3

A composite is produced from Titanium reinforced with aligned silicon carbide fibres. The elastic modulus of titanium is 118 GPa and silicon carbide 380 GPa. The composite contains approximately 50% titanium and 50% fibres.

a.Calculate the overall modulus of the composite, explaining your calculations and the assumptions you have made when it is loaded:

i.Along the direction of fibre length

ii.Perpendicular to the fibre length

b.Explain briefly why the material might show different yield behaviour in tension and compression when loaded cyclically.

c.A sample measuring 70mm x 1mm x 1mm made from the composite is loaded to an applied stress of around 300 MPa along the longitudinal direction (the dimension measuring 70mm). The strains are measured :

i.In the titanium matrix: +1400 με longitudinal; -430 με transverse

ii.In the SiC fibres: +650 με longitudinal; -75 με transverse

Calculate the longitudinal and transverse stresses in the two phases from the measured strains (assume that the longitudinal and transverse strains are the principal strain components, and that the two transverse strain components are equal, i.e. ₂ = ₃.) Take the values of Young's modulus and Poisson's ratio to be 118 GPa and 0.3 for the steel, and 380 GPa and 0.18 for the SiC.

d. Describe two possible methods an engineer could predict if each of the phases was yielding. Mention the pros and cons for both methods.