Reference no: EM13371396

Q.1. Clifton Distributing has three plants and four distribution centers. The plants, their supply, the distribution centers, their demands, and the distance between each location is summarized in the following table:

Distance	Center 1	Center 2	Center 3	Center 4	Supply
Plant A	45	60	53	75	500
Plant B	81	27	49	62	700
Plant C	55	40	35	60	650
Demand	350	325	400	375

 Draw the transportation network for Clifton's distribution problem. Formulate the LP model for Clifton assuming they wish to minimize the total product-miles incurred. Implement a spreadsheet model and use Excel Solver to obtain an optimal solution to the problem.

Q.2. A small town wants to build some new recreational facilities. The proposed facilities include a swimming pool, recreation center, basketball court and baseball field. The town council wants to provide the facilities which will be used by the most people, but faces budget and land limitations. The town has $400,000 and 14 acres of land. The pool requires locker facilities which would be in the recreation center, so if the swimming pool is built the recreation center must also be built. Also the council has only enough flat land to build the basketball court or the baseball field. The daily usage and cost of the facilities (in $1,000) are shown below.

Variable	Facility	Usage	Cost ($1,000)	Land
X1	Swimming pool	400	100	2
X2	Recreation center	500	200	3
X3	Basketball court	300	150	4
X4	Baseball field	200	100	5

 Formulate the ILP to maximize the daily usage of the recreational facilities. Implement a spreadsheet model and use Excel Solver to obtain a solution to the problem.

Q.3. ABC, Inc. produces two high-priced metal baseball bats, the Slugger and the Launcher, that are made from special aluminum and steel alloys. The cost to produce a Slugger bat is $100, and the cost to produce a Launcher bat is $120. We can not assume that ABC will sell all the bats it can produce. As the selling price of each bat model -- Slugger and Launcher -- increases, the quantity demanded for each model goes down.

Assume that the demand, S, for Slugger bats is given by S = 640 - 4P_Sand the demand, L, for Launcher bats is given by L = 450 - 3P_Lwhere P_S is the price of a Slugger bat and P_L is the price of a Launcher bat. The profit contributions are P_S S- 100S for Slugger bats and P_L L- 120L for Launcher bats. Develop the total profit contribution function for this problem.Implement a spreadsheet model and use Excel Solver to obtain a solution to the unconstrained problem.

Q.4. An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses. Annual demand is 20,000 units and each cartridge costs the store $25. It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item. What is the optimal ordering quantity?

Q.5. The drying rate in an industrial process is dependent on many factors and varies according to the following distribution.

Minutes	Relative Frequency
3	0.14
4	0.3
5	0.27
6	0.18
7	0.11

Use Excel to simulate 100 trials. What is the mean drying time from the 100 trials? Give summary statistics of the results.

  Q.6. An investor is considering 4 investments, A, B, C, D. The payoff from each investment is a function of the economic climate over the next 2 years. The economy can be weak or strong. The investor has estimated the probability of a declining economy at 30% and an expanding economy at 70%.

a. Draw the decision tree for this problem and determine the correct decision for this investor based on the expected monetary value criteria.

b. What decision should be made by the optimistic decision maker?

c. What decision should be made by the conservative decision maker?

d. What decision should be made under minimax regret?

	Payoff Matrix
	Economy
Investment	Weak	Strong
A	-30	120
B	20	60
C	30	35
D	15	30

ANS: 

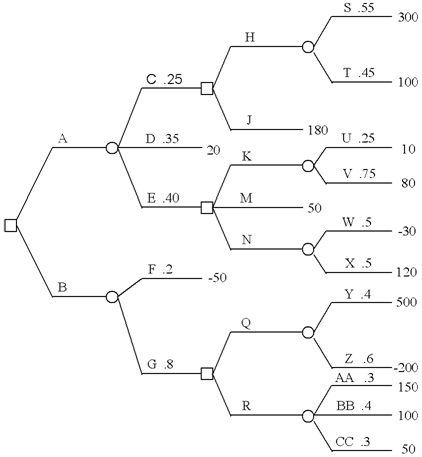
 Q.7. Fold back the decision tree and state what strategy should be followed. Show your work and explain the strategy.