Reference no: EM133360656

Question 1. Consider the inner product space F^m×n with inner product (A, B) = tr(B*A). Determine the angle (in radians) between the matrices

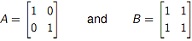
Question 2. Let A ∈ F^n×n be an invertible matrix and ||.|| be a norm on F^n×1. Prove that the mapping ||.||_A: F^n×1 → F defined by ||x||_A = ||Ax||for x ∈ F^n×1 is also a norm on F^n×1.

Question 3. Prove the polarization identity for real inner product spaces. That is, if V is an inner product space over R and x , y ∈ V , prove that 4(x , y) = ||x + y||² - ||x - y||².

Question 4. In this problem, we will prove the maximum absolute row sum formula for ||A||_∞. Let A ∈ F^m×n and let α = max_{1≤ i ≤m} Σⁿ_j=1 |a_ij|.

(a) Show that for any x ∈ F^n×1 with ||x||_∞ = 1, ||Ax||_∞ ≤ α.

(b) Suppose the kth row of A is the row with absolute sum equal to α. Find a vector y ∈ F^n×1 such that ||A||_∞ = α. (Hint. Define the entries of y in terms of appropriate entries of A = [a_ij]. Remember that for any z ∈ C, zz¯ = |z|² = |z¯|² and |z/|z|| = 1.)

Make sure you understand why parts (a) and (b) suffice to prove the maximum absolute row sum formula for ||A||_∞!