Reference no: EM133083999

Question 1: Let A be an infinite set. Prove that if there is a good ordinance ≤₁ in A, then there is a good ordinance ≤₂ in A, for which the well-ordered sets {A, ≤₁} and {A, ≤₂} are not isomorphic.

Question 2: Prove that for any set A the following are valid:

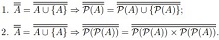
Question 3: Let {A,≤} be a linear ordered set. Let the function π:P(A)→P(A) be defined by:

π(X)={y∈A:seg(y)⊆X}

Prove that π is monotonic and if that A* is the smallest fixed point of π, then for each  x∈A the following equivalence holds:

x∈A∗<=>{seg(x),≤∩(seg(x)×seg(x))} is a well ordered set

Question 4: Prove that in {P (ω), ⊆} there are chains that are equinumerous with P (ω).

Question 5: Let X ⊆ R be well ordered by the usual ordinance in R. Prove that X is either finite or countable.

Question 6: A set A is finite exactly when each non-empty subset of P (A) has a maximum element in the sense of ⊆

Question 7: Let Φ(x) be a set-theoretic property. We will be saying that Φ is transitive on the ordinals

if:(∀α)(∀β)[α ∈ β => Φ(β) => Φ(α)] . Prove that if Φ is transitive on the ordinals, then:

For every ordinal α, for which ¬Φ(α) then (∀β)[Φ(β) ⇒ β < α];

If the set A, where (∀α)[α ∈ A ⇐⇒ Φ(α)], does not exist, then ∀α(Φ(α)).

Question 8: Let x be a set. Then x is an ordinal exactly then, when each personal transitive subset of x is an element of x.