Reference no: EM131085986

Assignment 4-

1. (a) For a ∈ Rⁿ and b ∈ R, prove {x ∈ Rⁿ: a^T x ≤ b} is convex.

(b) If P ⊂ Rⁿ is an n-dimensional polytope and F ⊂ P is a proper face, prove dim(F) < dim(P).

(c) If P ⊂ Rⁿ is bounded n-dimensional polytope, and the intersection of a finite number of half spaces, prove P is the convex hull of finitely many points. (Hint: Use induction on n).

(d) A face of a convex set S ⊂ Rⁿ is a convex subset F ⊂ S such that If x ∈ F and x = λx⁽¹⁾ + (1 - λ)x⁽²⁾ with λ ∈ (0, 1) and x⁽¹⁾, x⁽²⁾ ∈ S, then x⁽¹⁾, x⁽²⁾ ∈ F. Give an example of a non-empty convex set S and a non-empty face F of S such that F is not the intersection F ∩ H of F with a hyperplane H, where S lies on one side of H.

2. The Traveling Salesman Problem is a classical combinatorial optimization problem described as follows. A salesperson has to visit each of a set of cities exactly once, and return to the first one. Between any two cities i and j, there is a travel cost c_ij. The salesperson wants to do this while minimizing the total travel cost. Let G = (V, E) whose vertices are the cities and edges are the travel routes between the cities. Show that the following is an integer linear programming formulation for the traveling salesman problem:

3. Let D = (V, A) be a directed graph with vertex set V and directed edges A, with capacities ce for each e ∈ A. Let s, t ∈ V be fixed vertices. Prove that the optimal value of the following linear program is precisely the maximum st-flow in D:

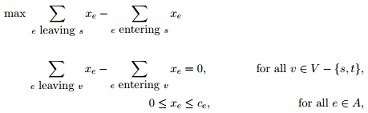
Note: We have not restricted xe to be integers apriori!

4. Recall the following proposed linear programming formulation for the stable set problem we gave in class:

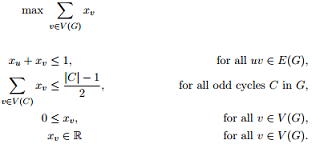
(a) Give an example of a graph for which this linear program has a solution that exceeds the maximum stable set in the graph.

(b) Give an example of a graph for which this linear program has a solution that exceeds the maximum stable set in the graph, if the following set of inequalities is added: ∑_{v∈V (Q)} x_v ≤ 1 for all complete subgraphs Q in G.

5. Use linear programming duality and Problem 3 to prove the Max-Flow Min-Cut Theorem.