Reference no: EM131085914

Assignment 1-

1. For a pair of vertices u, v in a graph G, the distance between u and v, denoted d(u, v), is the number of edges in the path from u to v using as few edges as possible. The diameter of G is

max_{u,v∈V (G)}d(u, v).

Let d, k be positive integers. Let G be a graph with maximum degree d and diameter k. Show that

|V (G)| ≤ 1 + d_i=0∑^k-1(d - 1)ⁱ.

Give an example of an G with (d, k) = (3, 2) where equality holds.

2. A cycle in a graph is Hamiltonian if it goes through all vertices. Suppose G is a graph on n vertices with the property that for every pair of vertices u, v that are not adjacent, deg(u) + deg(v) ≥ n. Prove that G has a Hamiltonian cycle. Can we replace n in the previous inequality by any value smaller than n and guarantee G is Hamiltonian?

3. Determine, with proof, the value of ex(n, K_1,r) for every pair of positive integers n, r.

4. (a) Suppose G is a graph not containing C₄ (a cycle on four vertices) as a subgraph. Prove that

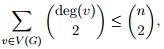
and use this to prove there is a constant C > 0 such that

ex(n, C₄) ≤ C · n√n, for all n ≥ 4.

(b) Let q be any prime and F_q be the finite field of order q. Consider the bipartite graph G_q with bipartition (P_q, V_q) where P_q is the set of 2-dimensional subspaces of F_q³ and V_q is the set of 1-dimensional subspaces of F_q³, with p ∈ P_q adjacent to v ∈ V_q if and only if v lies in p. Show that for any prime q, G_q does not contain C₄ as a subgraph, and

|E(G_q)| ≥ n√n/2√2,

where n = |V (G_q)|. Hence there is a constant C > 0 such that for infinitely many n,

ex(n, C₄) ≥ C · n√n.

Recall that for any graphs G₁, G₂, . . . , G_k, we define R(G₁, G₂, . . . , G_k) to be the smallest positive integer n so that for any k-coloring of the edges of Kn, say with colors c₁, c₂, . . . , c_k, there must exist some i for which G_i is a subgraph, all of whose edges are colored with color c_i. For simplicity, we denote R(K_r1, K_r2, . . . , K_rk) by R(r₁, r₂, . . . , r_k).

5. Let m, n be positive integers, and assume (m - 1)|(n - 1). Determine, with justification, a function f(m, n) for which R(T, K_1,n) = f(m, n) for every tree T on m vertices.

6. In this problem, we shall prove R(3, 4) = 9.

(a) Consider the graph G whose vertex set is {1, 2, 3, 4, 5, 6, 7, 8}, with i and j adjacent if and only if i - j = ±1 or ±4 mod 8. Show that G does not have K₃ and a subgraph, and G does not contain K₄ as a subgraph.

(b) Show that for any graph G on 9 vertices, either G has K₃ as a subgraph, or G has K₄ as a subgraph. (Hint: Consider three cases: The existence of a vertex with degree at least 4, the existence of a vertex of degree at most 2, and G being 3-regular).

7. (a) Show that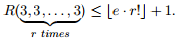

(b) Suppose the integers {1, 2, . . . , n} are partitioned into r disjoint sets A₁, A₂, . . . , A_r. Show that if n ≥ ⌊e · r!⌋ + 1, then one of the sets A_i contains three elements x, y, z such that x + y = z.