Reference no: EM131109292

2008 Honors Examination in Algebra

1. Decide whether each of the following statements is true or false. Give brief reasons or counterexamples to support your answer (full details unnecessary). If you have time, try to salvage any false statements (if appropriate), adding conditions or reworking the statement so that it would be true. Read the statements carefully!

(a) Let G be a group. If d divides the order of G, then G has a subgroup of order d.

(b) In a commutative ring, the intersection of any two prime ideals is also a prime ideal.

(c) The polynomial 4x² + 6x + 3 is a unit in Z₈[x].

(d) Any subring of a field is also a field.

(e) For every integer a > 0, x³ + ax + 1 is irreducible in Q[x].

(f) The number of Q-automorphisms of Q(4√ 2) is 4.

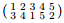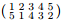(g) The permutations andare conjugate in the symmetric group S₅.

(h) The factorizations 10 = 2 · 5 and 10 = (1 + 3i)(1 - 3i) show that Z[i] is not a unique factorization domain.

(i) Every unique factorization domain is a principal ideal domain.

(j) A regular 340-gon is constructible using only straightedge and compass.

(k) Every symmetric polynomial in C[x₁, . . . , x_n] can be written uniquely as a linear combination of elementary symmetric polynomials.

(l) The matrix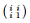is normal.

2. A subgroup H of a group G is called a characteristic subgroup if φ(H) = H for all automorphisms φ of G.

(a) Prove that every subgroup of a cyclic group is characteristic.

(b) Prove that the center of a group is characteristic.

(c) If H is a characteristic subgroup of K and K is a characteristic subgroup of G, must H be a characteristic subgroup of G?

3. For any commutative ring R, let Aff(R) =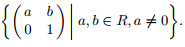

(a) For an odd integer m > 1, show that the commutator subgroup of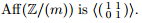

(b) Compute the number of p-Sylow subgroups of the group Aff(Z/(7)) for p = 3, 5, 7.

4. Construct a field of size 9, and find a generator for its nonzero elements.

5. Let G be a group of order pq, where p<q are primes with q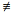1 mod p. Show that G must be cyclic.

6. Let A =define a bilinear form on R³ by (v, w) = v^tAw.

(a) Find a nonzero vector v ∈ R³ which is self-orthogonal, i.e., (v, v) = 0.

(b) Find an orthogonal (not necessarily orthonormal) basis of R³ for this bilinear form and compute the matrix for the bilinear form with respect to that basis.

7. Let X = {{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}} be the set of all 2-element subsets of {1, 2, 3, 4}. Let each permutation σ ∈ S4 act on the set X by the rule

σ({i, j}) = {σ(i), σ(j)},

where i ≠ j.

(a) Decompose X into orbits for the action of the subgroup of S₄ generated by (12).

(b) Decompose X into orbits for the action of the subgroup of S₄ generated by (123).

(c) Prove all the elements of S₄ act on X by even permutations.

8. Let I = (2, x) be the ideal generated by 2 and x in Z[x].

(a) Show that I is not principal.

(b) Show that I is maximal. (This does not need part (a).)

9. Let ζ = e^2πi/8 be a primitive 8th root of unity.

(a) Find the degree of the extension Q(i, 4√2) over Q and a Q-basis for it.

(b) Is Q(i, 4√2) = Q(i + 4√2)? Explain.

(c) Find the degree of the extension Q(ζ,4√2) over Q.

(d) Is Q(ζ,4√2) = Q(ζ + 4√2)? Explain.

10. An incomplete character table of a finite group G is given below; the number in parentheses above each element indicates the size of that element's conjugacy class. For example, the conjugacy classes of G are represented by 1, u, v, w, x, and y, and the conjugacy class of v contains 2 elements.

#Cg	(1)	(1)	(2)	(2)	(3)	(?)
g	1	u	v	w	x	Y
χ1	1	1	1	1	1	1
χ2	1	1	1	1	-1	?
χ3	1	-1	1	-1	i	?
χ4	1	-1	1	-1	-i	?
χ5	2	2	-1	-1	0	?
χ6	?	?	?	?	?	?

(a) Complete the character table and find the size of G.

(b) Show that u has order 2 and x has order 4.

(c) Show that v generates a normal subgroup of order 3.

(d) Show the representation corresponding to χ₆ is faithful.

(e) Show that w has order 6.