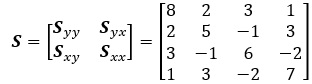Prove that a symmetric matrix has real eigenvalues

Assignment Help Other Subject

Reference no: EM132927928

Warm-up Activity

The goal of discriminant analysis according to Johnson and Wichern is

"To describe, either graphically (in three or fewer dimensions) or algebraically, the differential features of objects (observations) from several known collections (populations). We try to find ‘discriminants' whose numerical values are such that the collections are separated as much as possible".

Question 1. Consider two samples of data:

Find the discriminant function and use it (according to page 543) to classify a new data point x_new'=[2 7].

Principle-component analysis is concerned with explaining the variance/covariance structure of any sample through the linear combinations such variables with the main goal in mind of dimension reduction. If data is multicollinear this is the main tactic to tackle that issue. A main theoretical underpinning is the following fact:

Question 2. Prove that a symmetric matrix has real eigenvalues and that the eigenvectors corresponding to distinct eigenvalues are mutually orthogonal. Use this fact to prove that any symmetric matrix A can be spectrally decomposed into CDC' with D a diagonal matrix containing the eigenvalues and C the normalized eigenvectors arranged column-wise.

Question 3. Suppose the random variables X_1,X_2,X_3 have the population variance/covariance matrix:

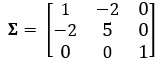
Calculate the principal components and interpret their meaning. What can be gained from knowing these values?

Numerical Questions

Instructions: Answer the following using the R statistical computing platform. Your answer should include the code you wrote plus the output of such code and English rhetoric / coding comments where necessary.

N1. Find the principle components for the stack loss dataset. Which component explains 85% of the variation in the original dataset?

N2. Perform a PCA on the iris dataset along the two lines: (i) the entire dataset, (ii) three subsets according to the three species. Check whether the PC scores are significantly different across the three species using an appropriate multivariate testing procedure.

N3. How do outliers effect PC scores? Perform a PCA on the board stiffness dataset with and without detected outliers.

N4. Canonical correlation analysis quantifies the correlation between a linear combination of variables in one set with a linear combination of potentially different variables in another set and maximizes such correlation among the space of linear combinations. Use equation (15.6) to give the sample canonical correlations if the sample covariance/variance matrix is:

Reference no: EM132927928

Questions Cloud

Find how much was yellow bell net income : Yellow Bell Co. also incurred expenses of $47,000, How much was Yellow Bell's net income assuming they used the accrual method of accounting?

Convert the projected GBP cash flows into Australian dollar : Convert the projected GBP cash flows into Australian dollar cash flows and calculate the NPV. Keep four decimal points when calculating forward exchange rates

What is involved in a performance gap analysis : What is involved in a performance gap analysis?

What was the material quantity variance for month of July : For the month of July, Beast Titan expected to produce 48,000 units. What was the material quantity variance for the month of July

Prove that a symmetric matrix has real eigenvalues : Prove that a symmetric matrix has real eigenvalues and that the eigenvectors corresponding to distinct eigenvalues are mutually orthogonal

How much were dividends for the year of quartz corporation : If revenues were $300,000 and expenses were $150,000, how much were dividends for the year assuming no other transactions affected retained earnings?

Why lifo method is not allowed in canada : Comment on the validity of the following statements: "As an asset loses its ability to provide services, cash needs to be set aside to replace it."

Organization for hr professional development : Based on critical evaluation and discussion with HR Professionals in your organization (Minimum 3 HR Professionals) create improved competency model which can b

What is the opportunity cost of seeing George Strait : Assume that there are no additional costs of seeing either show. Based on the information presented here, what is the opportunity cost of seeing George Strait

User Account

All Pages