Reference no: EM131207568

Q1. Give R code using the function rep() to create the following vectors?

(i) 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5

(ii) 1 2 2 2 2 2 3 3 4 4 5

Q2. Give R code using the function seq() to produce a vector of twenty increasing equally spaced points between -2 and 3.

Q3. Give R code to evaluate the following, without using loops

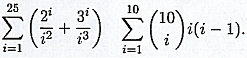
Q4. Provide R code which uses a loop to generate samples of size 100 from t-distributions with degrees of freedom equal to 1, 2, 4, 8, 16, 32 and stores them in the columns of a 100 x 6 matrix. Create a histogram of each sample, together with a normal probability plot complete with a line to assess how straight the Q-Q plot is. The plots should be arranged in a 2 x 6 array on a single graph sheet, with the histograms on the top row and the Q-Q plots in the bottom row. Each plot should have a title with an indication of the distribution (including degrees of freedom) used to generate the data.

Q5. Carefully describe what is accomplished by the following piece of R code, commenting on each line of the code:

x <- seq(-5, 5, by = 0.1)

y <- 3 + 1.2 * x + rnorm(length(x) , mean=0,sd=2)

par (pty=" s" )

plot(x, y, pch=1)

title(main="Plot of Response vs. Explanatory")

fit <- lm(y ~ x)

abline(fit)

summary(fit)

par(pty="m", mfrow=c(2, 2))

plot (fit)

Q6. Assume that Y is a numeric matrix with n rows and m columns. Describe in detail what is accomplished by the following R code:

Ym <- rep(0, m)

Ys <- rep(0, m)

for (j in (1:m)) {

Ym[j] <- mean (Y [, j] )

Ys[j] <- sd(Y[,j])

for (i in (1:n) ) {

Y[i,j]<- (Y[i,j] - Ym[j] ) /Ys[j]

}

}

How can you compute Ym and Ys and perform the same transformation on Y in a quicker and more transparent way?

Use the function scale () in conjunction with the function apply () to perform the same transformation on Y in a single line of code (without calculating the values of Ym and Ys).

Q7. Suppose that f(x) is a function defined for all x ∈  (0, 1) . Also, suppose that you do not know how to compute ₀∫¹ f(x)dx. One way to estimate the integral by simulation is as follows:

(i) randomly draw n points x in (0, 1);

(ii) generate the vector y such that y[i]=f (x[i]);

(iii) estimate the integral using the sample mean of y

I^{^} = y^-.

Write a R function sim.integ() which takes as arguments the function f and returns the above estimates I^{^} of ₀∫¹f(x)dx.

(b) Use your function to evaluate

₀∫¹x²sin(x) + tan(x) dx.

for n = 100, 1000, 10000, 100000.

(c) Calculate the integral using R's integrate() function. [The exact value of the integral is -2 + 2 * sin(1) + cos(1) - log(cos(1)) = 0.83887.]

Q8. Let y_t be a sequence of random variables that follows the moving average model of order 1:

y_t = ε_t + bε_t-1       t = 2, ..., N

where ε_t are i.i.d. N(0, σ²) and b is a known constant in the interval [-1, 1]. To define y₁, we set ε₀ = 0. According to this model, y_t is equal to a noise term ε_t plus (or minus, depending on the sign of b) some fraction of the noise term ε_t-1 at the previous time.

Write an R function MA1() that takes as arguments the final time N and the parameters b and σ and generates a sequence y_t from the model above, and plot four generated sequences in a 2 x 2 display.

The function should return a list with three components: b, sigma and a vector y containing the generated sequence. The function should check that N and o are positive and that b lies in the interval [-1, 1] and return an error if not.

Q9. Suppose that f(x) is a monotone function (i.e. strictly increasing or strictly decreasing) defined on an open interval of the real line and with a unique root x_r satisfying f(x_r) = 0. The root x_r can be found numerically using an iterative method known as the regula falsi or secant method. Given two values x_i and x_i-1, the method determines the secant line, i.e. the line that goes through the points (x_i-1, f(x_i-1)) and (x_i, f (x_i)). The next iterate x_i+1 is the value where the secant line cuts the x-axis, which is easily shown to be given by the following equation

x_i+1 = x_i - f(x_i)( x_i - x_i-1/f(x_i)-f(x_i-1)).

Write an R function regulafalsi 0 to implement the secant method. The arguments of regulafalsi () should include a function f() to providing the definition of f(x), and two values x₀ and x₁ to start the iterations.

Use the function regulafalsi() to solve the equation

x^1/2 + 3 log x = 5 x > 0.

numerically, starting at x = 1. Compare with the result of using the function uniroot() to find a solution in the interval (1,5).