Reference no: EM135372
Q1 Consider the Hire Assistant problem. We interview n candidates and always hire the best qualified so far. Let n = 5 for our example. Find the probabilities that we hire exactly 1 time, 2 times, 3 times, 4 times and 5 times. Define the probabilities as Pr(h=i), where i = 1 ... 5.
Q2 Repeat problem #1, but let n = 10. Find the expected number of candidates hired using your probabilities. You do not have to show each Pr(h=i), but you will need it for your E(H), where H = 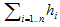
, and therefore E(H) = 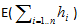 .
.
Q3 We have studied heaps and its relationship with complete binary trees and arrays which implement those binary trees. Consider a max-heap implementing a priority queue, as we did in class.
a. Explain the process of insertion into a heap-implemented priority queue, and informally explain its complexity.
b. Explain the process of removal from a heap-implemented priority queue, and informally explain its complexity.
Q4 Suppose we implement a priority queue, as a straight array, that is, the higher priority elements are ahead of any lower priority elements.
a. Informally, find the complexity of inserting and removal from this structure and compare it to the heap-implemented priority queue.
b. Suppose that you were to perform m1 insert operations and m2 remove operations from a straight array priority queue implementation. Describe in words the situation where the best and worst case complexity will occur. Create the mathematical model when the average case will occur.