Problems on advanced computer networks

Assignment Help Advanced Statistics

Reference no: EM1368355

Problem 1:

Suppose, we have a network in which data transfer requests (or flows) arrive for scheduling at a central server. Suppose that all the requests share a bottleneck link whose capacity is 70+X Mbps (Mega bits per second), where X = (Your roll number) modulus 20. The bottleneck link in the path of a flow is the link with the smallest available capacity. Suppose that the inter-arrival times of the requests (or flows) are exponentially distributed but the data size and the transfer duration of the flows is constant (same for all flows). The minimum required data transfer rate of a flow is obtained by dividing its data size with its transfer duration. The data transfer rate of a flow can increase (if bandwidth is available) during its transfer at any stage. The link is always fully utilized if there is at least one flow using that link. A request is rejected if its required transfer rate is not available at its arrival time.

a) Identify and explain the events that can change the state of the system

b) Suppose the arrival times of the first 10 requests are 1, 3, 5, 6, 7, 8, 11, 12, 14, 15 seconds (of simulation time). The data size of each flow is 180+Y Mega bits, where Y = (Your roll number) modulus 30, and the transfer duration of each flow is 5 seconds. Fill the following table.

MC	N = number of jobs	Request: accepted	Completion time of the
(master clock)	in the system	or rejected	request (if accepted)
0
1
3
5
6
7
8
11
12
14
15

Problem 2:

Jobs arrive at a server according to a Poisson input process at a rate of four per day, and the service time has an exponential distribution with a mean of 1/5 per day. Enough-in-process storage space is provided at the server to accommodate five jobs in addition to the one being processed. Determine the percent of time that this storage space will be adequate to accommodate newly arrived jobs.

Problem 3:

Traffic to a message switching center for one of the outgoing communication lines arrive exponentially at an average rate of 220 messages per minute. The line has a transmission rate of 880+B characters per second, where B = (Your roll number) modulus 40. The message length distribution (including control characters) is exponential with an average length of 170 characters. Hence, the service times of messages are also exponentially distributed. Calculate the following principal statistical measures of system performance, assuming that a very large-sized (infinity) message buffer is provided:

(a) Average number of messages in the system

(b) Average number of messages in the queue waiting to be transmitted.

(d) Average time a message waits for transmission

(e) Probability that 10 or more messages are waiting to be transmitted.

Problem 4: Extend (by 10 more rows) and fill the table. Consider two repairmen for the machine-repairmanproblem.

Operational time of each machine = 6+C units of time, where C = (Your roll number) modulus 3 Repair time for each machine = 6 units of time

CL1, CL2, CL3 are associated with machines 1, 2, 3 respectively CL_R1 and CL_R2 tell repairman 1's and 2's completion time respectively

At t=0, all three machines are operational, CL1=2, CL2=5, CL3=5+D units of time, where D = (Your roll number)modulus 3.

MC	CL1	CL2	CL3	CL_R1	CL_R2	N	R1	R2
0	2	5	5+D?	-	-	0	idle	idle

Problem 5: The CDF of exponential distribution is F(x) = 1-e-ax. Write a programming code to generate 100random variates according to exponential distribution and store them in an array.

Problem 6:

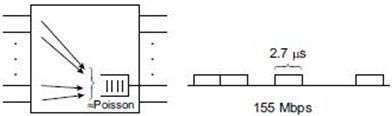
1663_Advanced Computer Networks.png

The output buffer of an ATM multiplexer can be modeled using a queue. Constant service time means that an ATM cell has a fixed size (53 octets; each octet is of 8 bits) and its transmission time to the link is constant. If the link speed is 155 Mbps, then the transmission time is S = 53* 8/155 μs = 2.7μs.

What is the mean number of cells in the buffer (including the cell being transmitted?) and the mean waiting time of the cell in the buffer when the average arrival rate on the link is 80+A Mbps, where A = (Your roll number) modulus 20?

Reference no: EM1368355

Questions Cloud

Positive and negative example of events : Can you select one positive and one negative example of events in your area, state, country or the world that might impact our life, careers or professions.

Define recently company has experienced issues with employee : Explain Recently your company has experienced issues with employee teamwork. Employees are not working well together. Your boss has asked you to research ways to create an effective team work environment.

Explain elements of enterprise information security policy : Write and explain briefly the three kinds of information security policy as described by NIST SP 800-14. Write and explain briefly four elements that must be present in Enterprise Information Security Policy.

Calculate opportunity cost of increasing the annual output : Atlantis is a small, isolated island in South Atlantic. The inhabitants increase potatoes and catch fresh fish. The accompanying table shows the maximum yearly output combinations of potatoes and fish that can be produced.

Problems on advanced computer networks : Identify and explain the events that can change the state of the system also determine the percent of time that this storage space will be adequate to accommodate newly arrived jobs-CS524 Advanced Computer Networks

Determine the expected number of empty bins : Assume that n balls are tossed into n bins, where each toss is independent and ball is equally likely to end up in any bin. Determine the expected number of empty bins?

Compute the npv and irr on properties : Compute the NPV and IRR on each of these properties individually and collectively assuming a discount rate of 15 percent

Determine the cost function : Manchester Foundry produced 45,000 tons of steel in March at a expenses of $1,150,000. In April, foundry produced 35,000 tons at a cost of $950,000.

Question on first degree price discrimination : Two consumers, Consumer 1 and 2, purchase the same product. Compute the prices that should be charged to each customer if the seller is able to use first degree price discrimination.

User Account

All Pages