Reference no: EM13834564

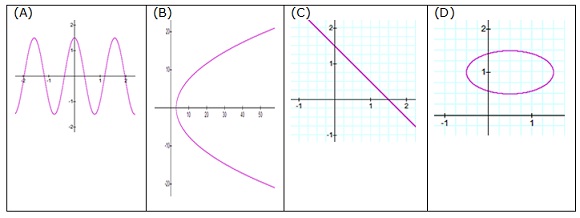
1. Which of these graphs of relations describe y as a function of x?

That is, which are graphs of functions? Answer(s): __A,C__________

(no explanation required.) (There may be more than one graph which represents a function.)

2. Consider the points (-7, 4) and (3, 6).

(a) State the midpoint of the line segment with the given endpoints. (No work required)

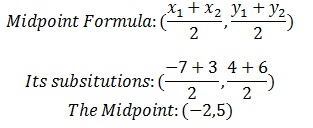
(b) If the point you found in (a) is the center of a circle, and the other two points are points on the circle, find the length of the radius of the circle. (That is, find the distance between the center point and a point on the circle.) Find the exact answer and simplify as much as possible. Show work.

3. Consider the following graph of y = f(x).

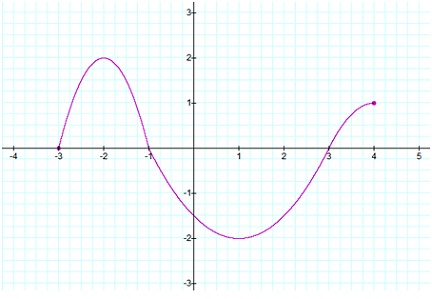
(a) State the x-intercept(s).

(b) State the y-intercept(s).

(c) State the domain.

(d) State the range.

4. Let f(x) = x - 9/x + 2

a. Calculatef(-3). (work optional)f(-3)=(-12)/(-3+2)

f(-3)=(-12)/(-1)

f(-3)=12

b. State the domain of the function

f(x) = (x - 9)/(x + 2)

(x+2)=0

x+2=0

(-∞,-2)∪(-2,∞)

c. Find f(a-1) and simplify as much as possible. Show work.

(x-9)/(x+2)=f(a-1)

(x-9)/(x+2)=f(a)+a(-1)

(x-9)/(x+2)=fa+f*-1

(x-9)/(x+2)=fa-f

(x-9)/(x+2)*(x+2)=fa*(x+2)-f*(x+2)

(x-9)/(x+2)*(x+2)/1=fa*(x+2)-f*(x+2)

(x-9)/1*1/1=fa*(x+2)-f*(x+2)

(x-9)/1=fa*(x+2)-f*(x+2)

x-9=fa*(x+2)-f*(x+2)

x-9=fa(x)+fa(2)-f*(x+2)

x-9=fax+fa*2-f*(x+2)

x-9=fax+2fa-f(x)-f(2)

x-9=fax+2fa-fx-2f

x-9=fax+2fa-fx-2f

We switched sides so the equals sign is right of the equation and the x's are closer together:

fax+2fa-fx-2f=x-9

fax+2fa-fx-2f-x=-9

afx-fx-x=-2fa+2f-9

x(af)-fx-x=-2fa+2f-9

x(af)+x(-f)-x=-2fa+2f-9

x(af)+x(-f)+x(-1)=-2fa+2f-9

x(af-f-1)=-2fa+2f-9

(x(af-f-1))/(af-f-1)=-2fa/(af-f-1)+2f/(af-f-1)-9/(af-f-1)

x=-2fa/(af-f-1)+2f/(af-f-1)-9/(af-f-1)

x=(-(2fa)+2f)/(af-f-1)-9/(af-f-1)

x=(2f(-(a)+1))/(af-f-1)

x=(2f(-a+1))/(af-f-1)-9/(af-f-1)

x=(-2fa+2f-9)/(af-f-1)

x=(-1(2fa)+2f-9)/(af-f-1)

x=(-1(2fa-2f)-9)/(af-f-1)

x=(-1(2fa-2f+9))/(af-f-1)

x=-(2fa-2f+9)/(af-f-1)

5. f is a function that takes a real number x and performs the following three steps in the order given:

(1) Multiply by 4.

(2) Subtract 8.

(3) Take the reciprocal. (That is, make the quantity the denominator of a fraction with numerator 1.)

(a) Find an expression for f(x). (no explanation required)

(b) State the domain of f. (no explanation required)

6. Given f(x)=x-3 and g(x)=√(x-1), which of the following is the domain of the quotient function ? Explain.

A. (1,∞)

B. [1,∞)

C. [1,3) u (3,∞)

D. (-∞,3) u (3,∞)

7. For income x (in dollars), a particular state's income tax T (in dollars) is given by

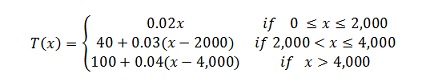
(a) What is the tax on an income of $3,200? Show some work.

(b) What is the tax on an income of $32,000? Show some work.

8. Let y = 8 - 2x².

a. Find the x-intercept(s) of the graph of the equation, if any exist. (work optional)

0=8-2x^2

8-2x^2=0

-2x^2=-8

2x^2=8

x^2=4

x=±√4

x=±√(2^2 )

x=-2,2x-intercept:(2,0),(-2,0)

b. Find the y-intercept(s) of the graph of the equation, if any exist. (work optional)

y=8-2(0)^2

y=8+0

y=8

y-intercept:(0,8)

c) Create a table of sample points on the graph of the equation. (Include at least five points.)

x	y	(x, y)
1	6	(1,6)
0	8	(0,8)
-1	6	(-1,6)
2	0	(2,0)
-2	0	(-2,0)

(d) Create a graph of the equation. (You may use the grid shown below, hand-draw and scan, or you may use the free Desmos graphing calculator described under Course Resource to generate a graph, save as ajpg and attach.)

(e) Is the graph symmetric with respect to the y-axis? _____ (yes or no).If no, state a point on the graph of the equation whose reflection fails to be on the graph, as done in section 1.2 homework in the textbook.

(f) Is the graph symmetric with respect to the x-axis? _no____ (yes or no).If no, state a point on the graph of the equation whose reflection fails to be on the graph, as done in section 1.2 homework in the textbook.

(-y)=8-2x^2

-y=8-2x^2

Not identical to original equation

(g) Is the graph symmetric with respect to the origin? __no___ (yes or no).If no, state a point on the graph of the equation whose reflection fails to be on the graph, as done in section 1.2 homework in the textbook.

(-y)=8-2x^2

-y=8-2x^2

y=-8+2x^2.

9. Letf(x) = 5x2 - 7x + 8 and g(x) = 1 - 3x.

(a) Find the difference function (f - g)(x) and simplify the results. Show work.

5x^2-7x+8-1+3x

5x^2-4x+8-1

5x^2-4x+7

(b) Find (g - f)(-1). Show work.

1-3x-5x^2+7x-8

-3x-5x^2+7x-9

-5x^2+10x+9

(c) Find (fg)(-1). Show work.

(1(5x^2 )+1(-7x)+1(8)-3x(5x^2 )-3x(-7x)-3x(8) )*-1

(5x^2-7x+8-15x^3+21x^2-24x)*-1

(26x^2-7x+8-15x^3-24x)*-1

(26x^2-31x+8-15x^3 )*-1

26x^2*(-1)-31x*(-1)+8*(-1)-15x^3*(-1)

26x^2 (-1)-31x(-1)+8(-1)-15x^3 (-1)

-26x^2+31x-8+15x^3

15x^3-26x^2+21x-8

10. The cost, in dollars, for a company to producexwidgets is given by C(x) = 4700 + 5.20x for  x > 0, and the price-demand function, in dollars per widget, is p(x) = 40 < 0.02x for 0 <x<2000.

(a) Find and interpret C(500).

(b) Find and interpret C ¯(500). (Note that C ¯(x) is the average cost function.)

(c) Find and simplify the expression for the revenue function R(x).(work optional)

(d) Find and simplify the expression for the profit function P(x).(work optional)

(e) Find and interpret P(500), where P(x) is the profit function in part (d).