Reference no: EM131449

All the data for this problem come from a conservative dialect of Vèneto, a Romance language spoken in northern Italy near the city of Padua. Since the language is related to Spanish, French and Italian, if you have studied or speak one of these languages the data will not be completely unfamiliar looking. But naturally this language has a different grammar, so your answers must be based only on the data provided.

The symbols used in the data should be familiar to you from the transcription of English, with the following exceptions:

1. Stress - if a vowel is stressed it is shown in the data with an acute accent mark, e.g. [á] is a stressed [a], [ε ] is a stressed [ε], etc.

2. In addition to the post-alveolar affricates [t' d'] which are like those of English, this language also has apical alveolar affricates [ts dz]. These are pronounced like [ts] and [dz] but, being affricates, they behave like single segments.

3. For convenience and ease of reading, in the data below the εap symbol [ε] has been replaced by an ordinary letter [r] (which normally represents a trilled [r]). Since the language does not have trilled [r] this substitution does not lead to any ambiguity.

Part I: Distribution Problem

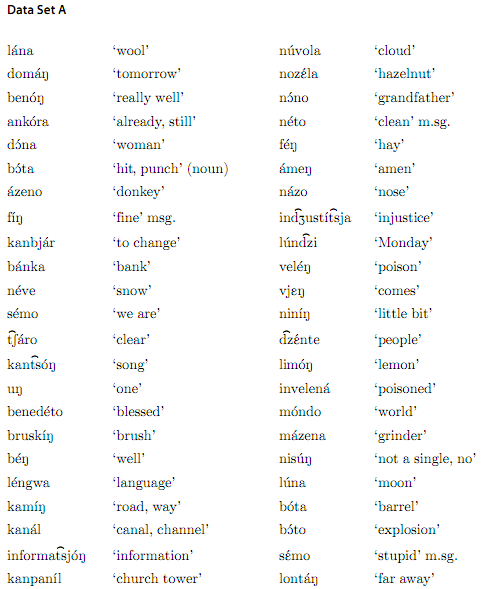
1. On the basis of the words in Data Set A, defend one of the two hypotheses below:

a. [n] and [η] are both underlying segments in Vèneto (i.e. they are ‘separate phonemes')

b. [n] and [η] are not both underlying segments; instead [n] and [η] are ‘allophones' of a single phoneme.

=> If you choose (a), show why a speaker of Vèneto would need to store the difference between [n] and [η] in memory; in other words, show that [n] is not a surface variant of [η], nor is [n] a surface variant of [n]. Put differently, show that [n] and [η] are not in complementary distribution but in contrastive distribution.

=> If you choose (b), explain how it could be possible that speaker of Vèneto could store only one of [n η] and their grammar could automatically derive the other. In other words, show that [η] and [ε] are in complementary distribution and that one of them could simply be a variant of the other in surface forms.

2. Answer the same questions as in question 1, but looking at the pairs [e ε] and [o ⊃]. 

=> Are [e] and [ε] in complementary or contrastive distibutionε What about [o ⊃]ε Provide speciεc examples from the data to support your conclusions.