Perform the matrix operations

Assignment Help Mathematics

Reference no: EM132907129

Question 1: Convert the following into the number systems specified:

(a) 1101111011001₂ to octal and hexadecimal forms.

(b) 3B4E5₁₆to denary and binary forms.

Question 2: Add the binary numbers, working in binary. Express the answer as an 8-bit number, clearly showing any carry bits.

11011110₂+ 01101101₂

Question 3: Follow the scenario and instructions clearly, and state the values as an exact value, or, correct to 2 decimal places accuracy:

(a) Given 2 complex numbers Z₁, Z₂ as:

Z₁ = 4 - 5j, Z₂ = -2 -3j

Find: Z = 3Z₁ + 2Z₂ in Cartesian form a + bj

(b) The current I in an a.c. circuit is given by I = j(0.5 - 2j)/7+5j

Find the current I in polar form r∠θ.

Question 4. Convert z = -?? + ?? to polar form and find z⁸ using De Moivre's theorem.

Plot z and z⁸ on an Argand diagram.

Question 5. The total impedance of two impedances connected in parallel is given by

1/z = 1/z₁+ 1/z₂

where z is the total impedance and z₁ = ?? + ??j and z₂ = ?? - ??j are the branch impedances.

Determine the current and its phase angle relative to a 110V supply voltage.

Question 6. Perform the matrix operations based on the given matrices:

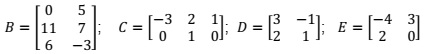
(a) B^T + C

(b) 3E - 2D^T

Question 7. Given the matrix

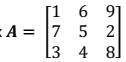
(a) Find the inverse of the matrix A clearly showing all the steps leading to the inverse matrix.

(b) Show clearly using matrix multiplication that AA^-1 = I and A^-1A = I, where I is the identity matrix.

Question 8. The system of currents i₁, i₂ and i₃ in a circuit satisfy these equations:

i₁ + i₂ + i₃ = 0
6i₁ - i₃ = 24
7 i₂ - 2i₃= 9

Solve the system using:

(a) Matrix inversion

(b) Gaussian elimination

Give the answers correct to 3 decimal places accuracy.

Reference no: EM132907129

Questions Cloud

Determine the probability of drawing : 1. There are 9 groups in your Data class and each group has to make a presentation on their Statistics Project. What is the probability that your group will go

How this value is shared between the parties involved : There has been considerable research undertaken to determine whether mergers really create value and, if so, how value is shared between the parties involved

Calculate the standard error : Calculate the standard error. May normality be assumed? (Round your answers to 4 decimal places.)

What are the steps in valuing a merger : Hager's management is new to the merger game, What are the steps in valuing a merger using the compressed APV approach

Perform the matrix operations : Determine the current and its phase angle relative to a 110V supply voltage and Find the inverse of the matrix A clearly showing all the steps leading

What is the current intrinsic value of vandell stock : Vandell pays a 40% combined federal and state tax rate. The risk-free rate of interest is 5%, What is the current intrinsic value of Vandell stock

What is the regression equation : Much of a stock price's movement can be attributed to the overall market (a rising tide lifts all boats, so to speak).

Find probability of the mean of samples : A sample of 35 items is randomly selected from this population. What is the probability that the mean of this samples lies between 72 and 79?

Explain the mean blood pressure : A researcher calculated the confidence intervals for the mean blood pressure of men and women from a very large sample, and found the following:

User Account

All Pages