Reference no: EM13844917

(1.) Assume that the random variable Y has pmf with parameter p, 0 < p < 1:

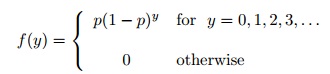
(a.) Find the cdf, F(y) for Y

(b.) Find the quantile function, Q(u) for Y

(2.) Let Y have a 3-parameter Weibull distribution, that is, Y has pdf and cdf in the following form with α > 0, γ > 0, θ > 0:

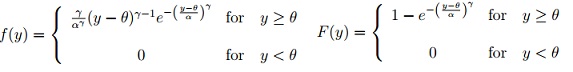
(a.) Verify that the pair (θ, α) are location-scale parameters for this family of distributions.

(b.) Derive the quantile function for the three parameter Weibull family of distributions.

(c.) What is the probability that a random selected value from a Weibull distribution with θ = 10, γ = 2 and α = 25 has value greater than 30?

(d.) Compute the 40th percentile from a Weibull distribution with with θ = 10, γ = 2 and α = 25.

( 3.) An alternative form of the 2-parameter Weibull distribution is given as follows with parameters β > 0, γ > 0

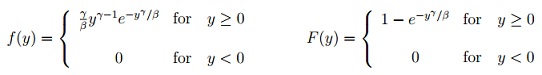
(a.) Show that β is not a scale parameter for this family of distributions?

(b.) Suggest a function of γ and β which would be a scale parameter for this family of distributions.

(4.) An experiment measures the number of particle emissions from a radioactive substance. The number of emissions has a Poisson distribution with rate λ = .25 particles per week.

(a.) What is the probability of at least 1 emission occurring in a randomly selected week?

(b.) What is the probability of at least 1 emission occurring in a randomly selected year?

( 5.) Let Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8 be independent N(0,1) r.v.'s. Identify the distributions of the following random variables.

(a.) R = Z 2 1 + Z 2 2 + Z 2 5 + Z 2 6.

(b.) W = Z7/ √ [Z 2 1 + Z 2 2 + Z 2 3 + Z 2 4 + Z 2 5 + Z 2 6 ]/6.

(c.) Y = 7Z 2 2 /[Z 2 1 + Z 2 3 + Z 2 4 + Z 2 5 + Z 2 6 + Z 2 7 + Z 2 8 ].

(d.) T = Z1/Z4.

(e.) S = 3(Z 2 2 + Z 2 4 )/[2(Z 2 1 + Z 2 3 + Z 2 5 )]

( 6.) (10 points) Let U = .38 be a realization from a Uniform on (0,1) distribution

Express a single realization from each of the following random variables using just the fact U = .38.

(a.) W = Weibull(γ=4, α=1.5)
(b.) N = NegBin(r=8, p=.7)
(c.) B = Bin(20, .4)
(d.) P = Poisson(λ=3)
(e.) U = Uniform on (0.3, 2.5)

(7.) For each of the following situations described below, select the distribution which best models the given situation. Provide a very short justification for your answer.

Hypergeometric Equally Likely Poisson Binomial Geometric Negative Binomial Normal Uniform Gamma Exponential Chi-square Lognormal Cauchy Double Exponential Weibull F t Logistic Beta

(a.) A wildlife biologist is studying if there is a difference between ducks in Texas and Michigan. She measures the wing span of each duck and then computes the difference between this wing span and a standard value for a large population of ducks. These differences are known to have a standard normal distribution. A sample of 100 ducks from Texas yield deviations, T1, . . . , T100. The total squared deviation from the standard value, i.e., T D = ∑100 n=1 T 2 i , is then computed. A similar statistic is computed for Michigan: MD = ∑100 n=1 M2 i . She now wants to compare the ratio R = TD MD to 1.0. The distribution of R is ?

(b.) The Geoscience Department at Stanford monitors the occurrences of earthquakes in the Northern Region of California. One of the variables of interest to the researchers is the length of time T between the occurrence of major earthquakes. The distribution of T is ?

(c.) A quality control engineer measures the difference D between the nominal diameter of a 5 cm ball bearing and the true bearing diameter. He finds that the bearings are equally likely to have a diameter larger than or smaller than 5 cm. Furthermore, 10% of the bearings have diameters which deviate more than 6 times their scale parameter from 5 cm. The distribution of D is ?

(d.) In the development of a new treatment for kidney disease in domestic cats, 100 cats with kidney problems are placed on the new treatment. The time T until the cat no longer has kidney disease is recorded for each of the 100 cats. A plot of the hazard rate function yields h(t) = 3.5t .8 . The distribution of T is ?

(e.) A manufacturer of computer hard drives ships the drives in boxes containing 30 drives. A box of hard drives is inspected by randomly selecting 6 hard drives from each box and testing the 6 drives for defectiveness. Let D be the number of defective hard drives found in a randomly selected box containing 30 hard drives. The distribution of D is ?

(f.) For each day during a six month period in Stamford, Connecticut, the maximum daily ozone reading R was recorded. The distribution of R is ?

(g.) A new type of transistor is in development. Using the data from an accelerated life test of the transistor, the failure rate function is found to be approximately a cubic function. Let T be the time to failure of the transistor. The distribution of T is ?

(h.) In proof testing of circuit boards, the probability that any particular diode will fail is known to be .001. Suppose a particular type of circuit board contains 200 diodes. Circuit boards are tested and the number N of failed diodes are recorded for each circuit board. The distribution of N is ?

(i.) A manufacture of spark plugs ships the plugs in packages of 100 plugs. A package is inspected by randomly selecting 5 plugs and testing whether or not the plugs are defective. Let N be the number of defective plugs in the sample of 5 plugs. The distribution of N is ?

(j.) The distribution of resistance for resistors having a nominal value of 10 ohms is under investigation. An electrical engineer randomly selects 73 resistors and measures their resistance. Based on these 73 values, she determines that the resistance R of the resistors has the following behavior: approximately 70% of resistors have resistance within one standard deviation of 10 ohms, 95% are within two standard deviations, and none of the resistors have resistance greater than three standard deviations from 10 ohms. The distribution of R is ?

(k.) A veterinarian is trying to recruit people to place their dogs in a study of the effectiveness of a new drug to control ticks on dogs. He needs 50 dogs in order for the study to meet professional standards of significance. Let M be the number of people the veterinarian interviews until he obtains the required 50 dogs for the study. The distribution of M is ?

(l.) The wings on an airplane are subject to stresses which cause cracks in the surface of the wing. After 1000 hours of flight the wing is inspected with an x-ray machine and the number of cracks N are recorded. The distribution of N is ?

(m.) Suppose small aircraft arrive at a certain airport according to a Poisson process with rate 8 aircraft per hour. For the next 100 days, the length of time, T, until the 15th aircraft arrives each day is recorded. The distribution of T is ?

(n.) A manufacturer of piston rings measures the deviation of the true diameter from the nominal value. This measurement is known to have a standard normal distribution. A sample of 10 rings yield deviations, X1, . . . , X10. The total squared deviation from the nominal value, i.e., W = ∑10 n=1 X2 i , is then computed. The distribution of W is ?

(o.) A large corporation has thousands of small suppliers of its raw materials. Let D be the proportion of parts in a randomly selected shipment that are defective. The vast majority of suppliers have small values of D but a few suppliers have large values of D. A possible distribution for D is ?