Reference no: EM131106209

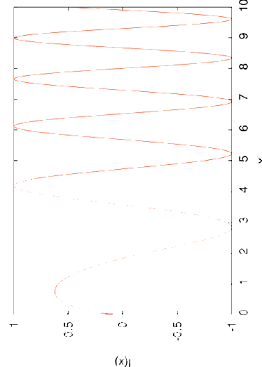
V. ASSIGNMENT 1 - OPTIMIZATION AND ROOT FINDING Often in physics it is desirable to find optimum conditions and to find the roots of functions numerically. The aim of this assignment is to investigate a function f(x), which is given by the formula f(x) = sin(x a − x 1 a + ax) (2) where the constant a is different for everybody, so that everybody is exploring a unique function. If you write down your student number (e.g. 12345678) then the last four digits (e.g. 5678) will be used to determine the value of a. • the value of a is 0.4 + (digits 5678 together)/25000 • for example, with the student number 12345678, a = 0.4 + 5678 / 25000 = 0.4 + 0.22712 = .62712 Note that for this function it is necessary that x ≥ 0 because f(x) will give complex results for x < 0. A. Assignment tasks 1. Plot y = f(x). Write a program to calculate f(x) for a range of x values with x ≥ 0. A function should be used to evaluate f(x). The results should be saved in a file of the type x0 f(x0) x1 f(x1) x2 f(x2) ...etc. where f(x0), f(x1), f(x2) etc. are the values of the function evaluated at regularly spaced x values x0, x1, x2, etc.

The data should be read in with Excel and plotted on a graph. The graph should run from x = 0 where f(x) = 0 and have a long enough range so that the function crosses the x-axis two or three times at larger values of x. [40] 2. Write a program to find roots where f(x) = 0 with the Newton-Raphson method. The first root is x = 0. Use the program to find the next two roots for f(x) = 0. The approximate positions of these next two roots should be visible from the graph you plotted. More accurate values can be found with the Newton-Raphson method. For the Newton-Raphson method you will need f ′ (x) ≡ df(x) dx , which is given by f ′ (x) = A cos(x a − x 1 a + ax) (3) where A = axa−1 − 1 a x 1 a −1 + a (4) The program should write each step of the iteration to a file with output x0 f(x0) f ′ (x0) x1 f(x1) f ′ (x1) x2 f(x2) f ′ (x2) ...etc. where x0 is the chosen start value of x, and f(x0) and f ′ (x0) are values of the function and gradient evaluated with x0; x1 is the refined estimate calculated from x0, f(x0) and f ′ (x0), and so forth. [30] 3. Find the most accurate value you can for the first maximum of f(x). The simplest way to do this is to use the program written for the first part of this assignment and hunt for it with that. The neatest solution, however, will be to find the maximum by either using the Newton-Raphson method to minimize f ′ (x) and/or by using the method of bisection. [30] B. What should be handed in Both paper and electronic submission is required for this assignment

1.       Paper report A paper report should be handed in with the following key points covered for each task. 1. Plot y = f(x). • A figure to show the plot of the function • A table with a few lines of output from the program with values of x from 0 to 0.1 in steps of 0.01; viz., x f(x) 0 f(0) 0.01 f(0.01) 0.02 f(0.02) ...etc. 0.1 f(0.1) 2. Find roots where f(x) = 0 • Clearly labelled results to show the values of x found for the roots where f(x) = 0. • A table few lines from the output from the Newton-Raphson optimization program; viz., x f(x) f ′ (x) x0 f(x0) f ′ (x0) x1 f(x1) f ′ (x1) x2 f(x2) f ′ (x2) ...etc. • The result from your NewtonRaphson optimization program of starting from x = 2; viz., x f(x) f ′ (x) 2 f(2) f ′ (2) x1 f(x1) f ′ (x1) x2 f(x2) f ′ (x2) ...etc. and a comment about how successful this was in reaching a root where f(x) = 0 3. Find the first maximum of f(x) • Your best value for the maximum of f(x) • A description of the method that you used to find the maximum with samples of data. 4. Appendix 

 

• A copy of each program used should be in the appendix clearly labelled. 2. Electronic submission You should submit • Electronic copies of the programs used in this assignment. • An electronic copy of your paper report. • An electronic copy of the Excel workbook used to make the plot for the first part of the assignment. C. Hints and notes • Do put plenty of comments in your programs to explain what each part of each program does. • In the Newton-Raphson method xn+1 = xn − f(xn) f ′ (xn) (5) • The Bisection method is more complicated to program, but has the advantage that it is not necessary to know f ′ (x). If x0 < x1 < x2 and f(x1) > f(x0) and f(x1) > f(x2) then there must be a local maximum between x0 and x2. This is a generally true rule. The Bisection method commences with three equally spaced x values x0, x1and x2 which satisfy the rule above. Now, two new x values are determined; x3 is placed midway between x0 and x1, and x4 is place midway between x1 and x2. f(x3) and f(x4) are evaluated. There are now five adjacent points x0 < x3 < x1 < x4 < x2; three adjacent points are chosen which satisfy the rule above and these three points are taken as the new x0, x1and x2 values. The same procedure is repeated until, ultimately, the space between the three values becomes so small it is insignificant.

 

Attachment:- Physics_C_1.pdf