Reference no: EM133338326
Mathematical Modeling
Assignment - Optimization and Linear Programming
Instructions
Read the following scenario, create and analyze a model as instructed, and present your model and analysis in a written report.
Case Scenario
Construction Co. typically bids on three types of projects: residential renovations, residential construction, and commercial construction. The company employs carpenters, electricians, plumbers, and drywallers, as these four trades cover the majority of the work in most projects. Work on projects that require other trades is subcontracted to other companies or tradespeople.
On average, a residential renovation requires a team consisting of a single carpenter, drywaller, plumber, and electrician. The average profit earned per renovation is $12,000.
Residential construction typically requires a team of three carpenters, four drywallers, one plumber, and one electrician. The average profit earned per residential construction project is $35,000.
On average, commercial construction projects require a team of 25 carpenters, 23 drywallers, 10 plumbers, and 10 electricians. The average profit earned per commercial construction project is $205,000.
You have been hired as a consultant by Construction Co. to determine how the company can maximize its profits, as detailed below. Your job is to explain both how to solve your client's problems and how you arrived at your solutions.
Part 1
Formulate and solve a linear programming problem to determine the number of each type of project the construction company should accept to maximize its profits.
Part 2
Market research suggests that Construction Co. can increase the rates it charges by up to 5%, 2%, and 15% for residential renovations, residential construction, and commercial construction, respectively, without affecting demand. Design and implement a sensitivity analysis to determine if the company should increase the rates it charges for residential renovations, residential construction, and/or commercial construction and determine the amount by which to increase the rates. Describe the change in the optimal number of each type of project the company should accept based on the new rates.
Construction Co. is also considering adjusting its labour force by hiring additional employees in the trades (carpenters, drywallers, plumbers, and electricians). Design and implement a sensitivity analysis to determine which trades, if any, should be hired and determine the maximum rate the company can pay each additional carpenter, drywaller, plumber, and electrician while remaining profitable.
Format
Combine parts 1 and 2 into a single submission that includes the Microsoft Excel spreadsheet you used to construct and analyze your model, as well as your written report.
Report
Present your model and analysis in a written report that includes the following sections:
Introduction: Begin by clearly stating the problem. Explain why it is appropriate to address the problem as a linear programming problem.
Methods: Outline the methods you used to identify a solution to the problem outlined above. For the sensitivity analysis, consider providing one or more figures depicting the design of the analysis.
Provide enough information that another modeler can understand what you have done and can validate your process.
Results: Carefully explain the results of your analysis, supporting it with relevant figures, tables, etc. as needed.
Conclusions: Briefly restate the main findings of your analysis, identifying the best strategies for Construction Co. to adopt.
Part 3
Instructions
Read the following scenario, create and analyze a model as instructed, and present your model and analysis in a written report.
Scenario
Problem 1: Maximum Flow
Figure 5.3.1 depicts a pipeline network as a set of nodes, which represent pumping stations, that are connected by a series of arrows, which represent the pipelines between the pumping stations. Flow through the pipeline is unidirectional from node to node, as indicated by the arrows. Each pipeline's capacity (maximum rate of flow) is indicated beside the corresponding arrow.
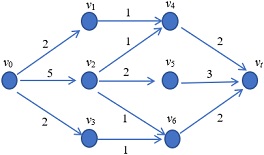
Figure 5.3.1. A pipeline network
Using the information provided, determine the maximum flow through the pipeline network.
Problem 2: Expected Maximum Flow
In addition to capacities, maintenance data is also available. Each day, any given pipeline may need to be shut down for a period of time for maintenance, reducing the pipeline's capacity for that day. The maintenance may be major or minor. Major maintenance requires a greater period of downtime than minor maintenance, resulting in greater reductions in capacity. A portion of the network's maintenance data is summarized in Table 5.3.1.
|
Line
|
Probability that maintenance is required for the day
|
Probability that required maintenance is major or minor
|
Reduced capacity during maintenance
|
|
v0 -v1
|
5%
|
Minor: 80%
Major: 20%
|
1
0
|
|
v5 -vt
|
8%
|
Minor: 50%
Major: 50%
|
2
1
|
|
v0 -v2
|
5%
|
Minor: 80%
Major: 20%
|
3
0
|
Table 5.3.1. Maintenance data
Based on the maintenance data provided, find the expected maximum possible flow through the pipeline network. If possible, also create a distribution of maximum possible flows for any given day, month, and year.
Format
Submit a written report detailing your solutions to Part 3 of this assignment. Your report should include the following sections:
Introduction: Begin by clearly stating the problem and explaining how it can be framed as an optimization problem. Then explain how Problem 1 is modified by the inclusion of the maintenance data and outline what considerations must be made in response.
Methods: Outline the methods you used to determine the maximum flow and the expected maximum flow of the pipeline network. If the methods you used to solve Problem 1 differ from those you used to solve Problem 2, explain why they are different. If you used simulation modeling, consider providing a figure depicting the logic of the simulation process.
Results: Carefully explain your solutions to Problems 1 and 2, supporting them with relevant proofs, calculations, figures, etc. as needed.
Conclusions: Briefly restate the main findings of your analysis as they relate to Problems 1 and 2. Along with your report, you may also include any Excel files you created for Part 3 of this assignment.