Reference no: EM131591

You will need to model each population in terms of a ?nite number of individuals which can increase or decrease each year with certain probabilities. Here a large value of the maximum population size, K , would be 20-50, but you should certainly start off which much smaller values (perhaps around 5 for each population) when getting your algorithmworking.

This model will only be counting females since they are the ones who can increase population.

Survival

Each year a female has a probability  of dying (so a probability of (1 ) of surviving). If the current population is j then the probability, si ,j , of having i surviving females after one year is given by the Binomial formula

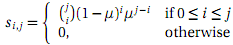
The si ,j values make up the (K +1)(K +1) survival matrix, S. For example, when K = 2 and  = 0.13 thematrix is

So if the current population is 0 then the probability is 1 that it will still be 0 next year. If the current population is 2 then the probability is 0.0169 that itwill be 0 (and thus extinct) next year.

This is a Markov chain transition matrix. Each column is a distribution that sums to 1, the probabilities of moving to the different states of the system in the next step. You can multiply a state vector by a transition matrix to get the distribution of probabilities for the next year. For example, having a current population of 2 is represented by the state vector

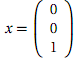
That is, we're 100% sure we are currently in state 2. Calculating Sx gives

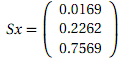
This means that after one year we have a 0.0169 chance of being extinct, as noted above. The nice thing about this matrix representation is that we can then see what happens another year on bymultiplying this vector by S again:

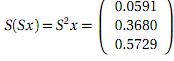
In general, St gives the cumulative transitionmatrix for t steps, in this case t years. For example,

so, if we started with 2 females, after 10 years we'd have a 56.49% chance of being extinct. If we started with only 1 it would be 75.16%.

Research Questions

Submit a report that addresses the following questions:

1. Why does a ?nite population with  >  tend to go extinct?

2. Use the given parameters to calculate examples of AZ and AW for small population sizes, such as KZ = 6 and KW = 14.

3. We will use stochastic dynamic programming (SDP) to ?nd the optimal decisions that maximize the probability that the wild population will not go extinct. The starting point for the recursion will be some time in the future when the conservation work ?nishes. To calculate the return function for this ?nal stage use A10 W to obtain the probabilities of going extinct after 10 years for various values of the ?nal wild population, nW.

4. Each year we can decide to capture animals, release animals, or do nothing. Ignoring the effect of capture/release on survival, use SDP backwards for around 20 years to determine the optimal strategy for various starting conditions (in terms of current wild and captive populations).

5. Interpret and discuss your solution. Change the parameter values ( and ) to see how the solution changes.

6. Extend your model to incorporate the deleterious effects of capture/release on survival.

For example, animals that are translocated might have an additional 0.05 probability of death in the ?rst year. Discuss how this value affects the optimal strategy.