Reference no: EM1396144

1. An iron rod of length L = 0.5 m, diameter D = 0.02 m, thermal conductivity k = 50W/(m ⁰C) protruding from wall is exposed to an ambient at T_∞ = 30 ⁰C. The heat transfer coefficient between the ambient and the rod surface is h= 100 W/(m^{2 0}C) and the base of the rod is kept at a constant temperature T₀ = 330 ⁰C. Assuming a one-dimensional steady-state heat flow, the mathematical formulation of this problem is given by the following equations:

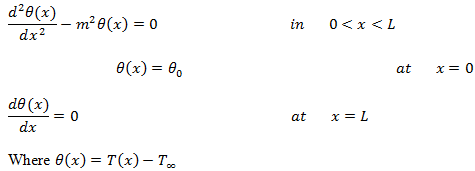
The finite difference approximation of this problem using 10 equal sub-regions (n = 10), is given by:

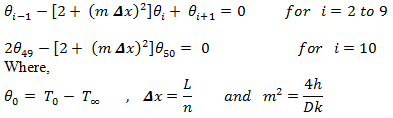
Where,

Now, find out the temperature differences at each locations (i.e. find out θ₁, θ₂, θ₃, θ₄, and θ₅ ) solving the finite difference equations using Gauss Elimination method. Also calculate the temperatures at each locations (i.e. calculate T₁, T₂, T₃, T₄, T₅...........) where T_i = θ_i + T_∞ Plot the temperature (T) versus location (x).

2. Repeat the above analysis for 20 equal sub-regions. Plot T vs. x. Compare (1) and (2).

3.  For n=20 case, extract the subdomain 4:10 rows and print the matrix for subdomain.