Reference no: EM132401009

International College of Engineering and Management
Programme: BSc (Hons) Fire Safety Engineering
Module Code: OM 2027
Module Title: Mathematics - 2

Question 1:
a. Explain the difference between integral and differential calculus?
b. Explain the uses of integration in real life.

Question 2:
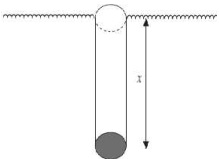
In order to calculate how much rope we must attach to a bucket to reach the water in a deep well as shown the figure below. A stone is dropped down the well and a splash is heard after two seconds. The acceleration of the stone is a = 9.8m/s² Determine:
a. A formula for the velocity
b. A formula for the depth
c. The depth of the well
Assume at t = 0, the velocity v = 0 and depth x = 0.

Question 3:

The power, P, in a circuit is given by:

P = ωR/2Π ₀∫^2Π/ω (i²)dt

Where: i = I sin (ωt), R is resistance and ω is angular frequency.

Show that:

P = I²R/2

Question 4:

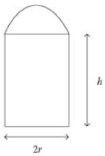
A glass window consists of a rectangle with sides of length 2r cm by h cm and a semicircle of radius r cm as shown in Figure below. The total area of one surface of the glass is 500cm².

a. Show that the perimeter P of the window is given by:

p = (2 + Π/r)r + 500/r

b. Determine the value of r for which P has a stationary value and hence determine its nature.

Question 5:

The acceleration of a body when time t = 0 second, the distance s = 40 meter and the velocity v = -10 m/s, is given by the following formula:

a = 20 t m/s²

Determine the position and velocity of the body at t = 3 seconds?

Question 6:

When t = 0, the position of a point is s = 6 m and its velocity is v = 2 m/s. From t = 0 to t = 6 s, the acceleration of the point is a = 2 + 2t². From t = 6 s until it comes to rest, its acceleration is a = -4 m/s².
i. What is the total time of travel?
ii. What total distance does the point move?