Reference no: EM131762241

Problem (The Brachistochrone 1-Problem) 1 -

The compound Greek word brachistochrone means minimal time. A bead slides down a wire that connects two fixed points. The goal is to find the shape of the wire in such a way that, starting from rest, the bead slides from one end to the other in minimal time. Simple guesses for the wires optimal shape, including a straight line, a parabola, a circular arc, or even a catenary are wrong.

Can you do better through a careful analysis of the associated variational problem?

Lets take, without loss of generality, the starting point of the bead to be at the origin: a = (0, 0). The wire will bend downwards, and so, to avoid distracting minus signs in the subsequent formulae, we take the vertical y axis to point downwards. The shape of the wire will be given by the graph of a function y = u(x) ≥ 0. The end point b = (α, β) is assumed to lie below and to the right, and so α > 0 and β > 0. The set-up is sketched in the figure.

Hints: 1) To mathematically formulate the problem, the first step is to find the formula for the transit time of the bead sliding along the wire. If v(x) denotes the instantaneous speed of descent of the bead when it reaches position (x, u(x)), then the total travel time is

T[u(·)] = ₀∫¹ ds/v = ₀∫^α√(1+(u')²)/v dx

where ds = √(1+(u')²) dx is the usual arc length element, and I is the overall length of the wire.

2) Use conservation of energy to determine a formula for the speed v as a function of the position along the wire. The kinetic energy of the bead is ½mv² and potential is -mgy = -mg u(x).

Problem 2 -

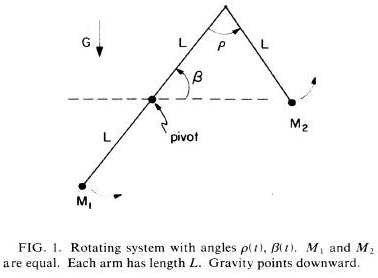
Consider a dynamical system shown in the Figure-1, which spins around its central point. β(t) denotes the angle between the central bar and the horizontal. ρ(t) denotes the angle between the central bar and the hanging pendulum. Both the masses are equal M₁ = M₂ = M and the motion is planar. The dynamics of this system as it spins around its central point can be extremely complex due to exchange energy between the modes of rotation. Show all the results/derivations explicitly for full marks.

• Obtain the Hamilton equations of motion.
• In absence of gravity, show that there is a second constant of motion and write the equation for the constant energy-surface
• Show that the system is integrable and show that

ρ^·(t) = ±[((6E₀-C₁²)-4E₀cos(ρ(t)))/(2-cos²(ρ(t)))]^½

where E₀ is the total energy with zero gravity and C₁ is second constant of motion.

Problem 3 -

(a) Prove the following theorem that charaterizes the asymptotic stability of the origin in terms of the Lyapunov equation.

Theorem: A matrix A is a stability matrix, that is, Re(λ_i) < 0 for all eigenvalues of A, if and only if for any given positive definite symmetric matrix Q there exists a positive definite symmetric matrix P that satisfies the Lyapunov equation

PA + A^TP = -Q.

Moreover, if A is a stability matrix, then P is the unique solution of the Lyapunov equation.

(b) Consider the second order system

x^·₁ = x₁ - x₂ - x₁(x₁² + x₂²),              x^·₂ = x₁+ x₂ - x₂(x₁² + x₂²),                     (1)

Show that M = {x ∈ R² : ||x|| = 1} is an asymptotically stable limit cycle (Except if staring at (x₁, x₂) = (0, 0)). Hint: take V(x) = (x₁²  + x₂² - 1)².

(c) Consider the second order system

x^·₁ = -2x₁+ x₁x₂,                               x^·₂ =-x₂ +x₁x₂,                                          (2)

Find the equilibrium points and determine their linearized stability? Find the positive definite matrix P by solving the Lyapunov equation for the stable equilibrium point with Q = I.

* Use V(x) = x^TPx as the Lyapunov function and determine the largest region B_r about the stable fixed point where the nonlinear system is asymptotically stable - which is called the domain of attraction (all graduate students taking the course for 4 units must complete this part of the question, however, extra points will be given for undergraduates and graduate students taking the course for 3 units).