User Account

All Pages

Nash equilibrium in the repeated prisoners dilemma game

Assignment Help Game Theory
Reference no: EM13815291

Unless stated otherwise, in the following problems assume that games considered are games of repeated Prisoner's Dilemma with stage payoffs of 0, 1, 3 and 5, that is

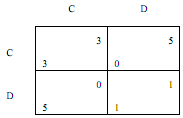
346_Games of repeated Prisoners Dilemma.png

Problem 1:

Consider the following strategy "Tit for Two Tats" (TF2T): Cooperate in periods 1 and 2. Thereafter defect in any period k>2 if and only if your opponent defected in k-1 and k-2.

(a) Consider best response strategies to TF2T in a discounted repeated game with δ sufficiently close to zero.

Is it possible to construct two strategies, j and j*, such that both of them are best responses to TF2T and (TF2T, j) is in Nash equilibrium while (TF2T, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

(b) Consider best response strategies to TF2T in a discounted repeated game with δ sufficiently close to one.

Is it possible to construct two strategies, j and j*, such that both of them are best responses to TF2T and (TF2T, j) is in Nash equilibrium while (TF2T, j*) is not? YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

(c) Consider best response strategies to TF2T in a repeated game without discounting (the payoff is an average per period payoff.)

Is it possible to construct two strategies, j and j*, such that both of them are best responses to TF2T and (TF2T, j) is in Nash equilibrium while (TF2T, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

Problem 2

Recall the strategy "Virgin" (V): V defects unconditionally in the first ten periods and then from period eleven on V cooperates unconditionally if and only if the opponent cooperated in all ten initial periods, and defects unconditionally otherwise.

(a) Consider best response strategies to V in a discounted repeated game with δ sufficiently close to zero.

Is it possible to construct two strategies, j and j*, such that both of them are best responses to V and (V, j) is in Nash equilibrium while (V, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

(b) Consider best response strategies to V in a discounted repeated game with δ sufficiently close to one.

Is it possible to construct two strategies, j and j*, such that both of them are best responses to V and (V, j) is in Nash equilibrium while (V, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

(c) Consider best response strategies to V in a repeated game without discounting (the payoff is an average per period payoff.)

Is it possible to construct two strategies, j and j*, such that both of them are best responses to V and (V, j) is in Nash equilibrium while (V, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

Problem 3

Recall the strategy "Casanova" (CA): C cooperates unconditionally in the first fifteen periods and then from period sixteen on it defects unconditionally.

(a) Consider best response strategies to CA in a discounted repeated game with δ sufficiently close to zero.

Is it possible to construct two strategies, j and j*, such that both of them are best responses to CA and (CA, j) is in Nash equilibrium while (CA, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

(b) Consider best response strategies to CA in a discounted repeated game with δ sufficiently close to one.

Is it possible to construct two strategies, j and j*, such that both of them are best responses to CA and (CA, j) is in Nash equilibrium while (CA, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

(c) Consider best response strategies to CA in a repeated game without discounting (the payoff is an average per period payoff.)

Is it possible to construct two strategies, j and j*, such that both of them are best responses to CA and (CA, j) is in Nash equilibrium while (CA, j*) is not?

YES NO (circle one)

If your answer is YES then give an example of two strategies like that. Whenever possible use the strategies defined in the lecture notes, otherwise define a strategy of your own.

j = .................

j* = .................

Problem 4

In the following problem assume that the game is that of infinitely repeated Prisoner's Dilemma with one-shot payoffs of 0, 1, 3 and 5 and without discounting (payoffs are calculated as per- period average.)

BR below stands for Best Response.

Are the following statements true of false? Circle the correct answer.

(1) If a pair of strategies (i,j) is such that i=BR(j) then u(i,j) ≥ 3. TRUE FALSE

(2) If a pair of strategies (i,j) is such that j=BR(i) then u(i,j) ≥ 3. TRUE FALSE

(3) If a pair of strategies (i,j) is such that i=BR(j) then u(i,j) ≥ 1. TRUE FALSE

(4) If a pair of strategies (i,j) is such that j=BR(i) then u(i,j) ≥ 1. TRUE FALSE

(5) If a pair of strategies (i,j) is such that i=BR(j) then u(i,j) < 5. TRUE FALSE

(6) If a pair of strategies (i,j) is such that j=BR(i) then u(i,j) < 5. TRUE FALSE

(7) If a pair of strategies (i,j) is in Nash equilibrium then u(i,j) ≥ 3. TRUE FALSE

(8) If a pair of strategies (i,j) is in Nash equilibrium and u(i,j)>3 then u(j,i)<3. TRUE FALSE

(9) If a pair of strategies (i,j) is in Nash equilibrium and u(i,j)<3 then u(j,i)>3. TRUE FALSE

(10) If a pair of strategies (i,j) is in Nash equilibrium then u(i,j) ≥ 1. TRUE FALSE

(11) If a pair of strategies (i,j) is in Nash equilibrium then u(i,j) ≤ 3. TRUE FALSE

(12) If a pair of strategies (i,j) is in Nash equilibrium then u(i,j) < 5. TRUE FALSE

Consider now the following strategies in an infinitely repeated Prisoner's Dilemma game: ALL D: defect unconditionally in all iterations of the game; ALL C: cooperate unconditionally in all iterations of the game; TFT (tit for tat): cooperate in the first interaction and then cooperate if the other player cooperated on the previous interaction and defect if he defected; STFT (suspicious tit for tat): defect in the first interaction and then cooperate if the other player cooperated on the previous interaction and defect if he defected; MACHO defect in the first iteration; in second iteration cooperate if the other player defected in the first iteration and then play "tit for tat"; if he cooperated in the first iteration, defect unconditionally in all periods of the game from iteration 2 onwards.

Problem 5

Consider an infinitely repeated Prisoner's Dilemma game with values of δ sufficiently close to (but not equal to) 0. Which of the following are true?

(1) ALL D is a best response strategy to TFT TRUE FALSE

(2) MACHO is a best response strategy to MACHO TRUE FALSE

(3) TFT is a best response strategy to TFT TRUE FALSE

(4) ALL D is a best response strategy to MACHO TRUE FALSE

(5) ALL D is a best response strategy to ALL C TRUE FALSE

(6) ALL C is a best response strategy to TFT TRUE FALSE

(7) STFT is a best response strategy to ALL D TRUE FALSE

(8) STFT is a best response strategy to STFT TRUE FALSE

Consider now an infinitely repeated Prisoner's Dilemma game with values of δ sufficiently close to 1. Which of the following are true?

(9) ALL D is a best response strategy to TFT TRUE FALSE

(10) MACHO is a best response strategy to MACHO TRUE FALSE

(11) TFT is a best response strategy to TFT TRUE FALSE

(12) ALL D is a best response strategy to MACHO TRUE FALSE

(13) ALL D is a best response strategy to ALL C TRUE FALSE

(14) ALL C is a best response strategy to TFT TRUE FALSE

(15) STFT is a best response strategy to ALL D TRUE FALSE

(16) STFT is a best response strategy to STFT TRUE FALSE

Problem 6

Which of the following pairs of strategies are in Nash equilibrium in the repeated Prisoner's Dilemma game without discounting? Circle YES if a pair is in Nash equilibrium and NO otherwise.

(MACHO, MACHO) YES NO
(TFT, STFT) YES NO
(ALL D, ALL D) YES NO
(TFT, TFT) YES NO

Problem 7

The game below is similar to the game of Chicken (aka Hawk and Dove.) Suppose it is a stage game of an infinitely repeated game without discounting (the payoff is an average per period payoff.)

Using the coordinate system below draw a "folk theorem diagram" i.e., a diagram that shows which pairs of payoffs are possible in the game and which pairs of payoffs are possible in Nash equilibria of this game. Mark all necessary numerical values in the coordinate system.

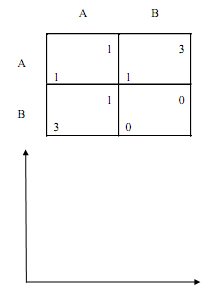
871_Games of repeated Prisoners Dilemma1.png

Problem 8

The game below is similar to that of Prisoner's Dilemma. Suppose it is a stage game of an infinitely repeated game without discounting (the payoff is an average per period payoff.)

Using the coordinate system below draw a "folk theorem diagram" i.e., a diagram that shows which pairs of payoffs are possible in the game and which pairs of payoffs are possible in Nash equilibria of this game. Mark all necessary numerical values in the coordinate system.

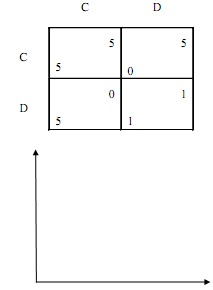
992_Games of repeated Prisoners Dilemma2.png

Problem 9

The game below is similar to the Pareto Coordination game. Suppose it is a stage game of an infinitely repeated game without discounting (the payoff is an average per period payoff.)

Using the coordinate system below draw a "folk theorem diagram" i.e., a diagram that shows which pairs of payoffs are possible in the game and which pairs of payoffs are possible in Nash equilibria of this game. Mark all necessary numerical values in the coordinate system.

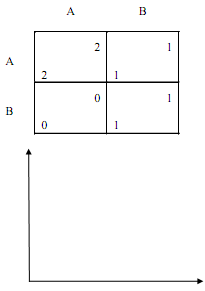
2411_Games of repeated Prisoners Dilemma3.png

Problem 10

(1) Consider the following game.

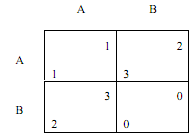
91_Games of repeated Prisoners Dilemma4.png

Suppose that what evolves in an evolutionary game are strategies (both pure and mixed) in a one- shot game depicted above.

Is pure strategy A an ESS? (Circle one.) YES NO

Is pure strategy B an ESS? (Circle one.) YES NO

(2) Consider the following coordination game:

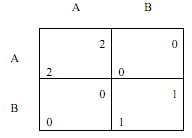
1406_Games of repeated Prisoners Dilemma5.png

Suppose that what evolves in an evolutionary game are strategies (both pure and mixed) in a one- shot game depicted above.

Is pure strategy A an ESS? (Circle one.) YES NO

Is pure strategy B an ESS? (Circle one.) YES NO

(3) Consider the following Chicken aka Hawk-Dove game (strategies denote choosing "aggress" (B) or "not aggress" (A)):

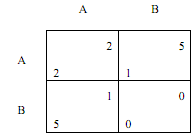
509_Games of repeated Prisoners Dilemma6.png

Suppose that what evolves in an evolutionary game are strategies (both pure and mixed) in a one- shot game depicted above.

Is pure strategy A an ESS? (Circle one.) YES NO

Is pure strategy B an ESS? (Circle one.) YES NO

Problem 11

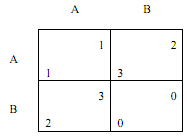
2239_Games of repeated Prisoners Dilemma7.png

Consider now an evolutionary game where what evolves are not strategies in a one-shot game but strategies in a repeated game without discounting. The stage game of the repeated game is given above. Consider only pure strategies in this repeated game. (WESS stands for weak ESS.)

(a) Is strategy ALL A ("play A unconditionally in all iterations of the game") an WESS? (Circle one.) YES NO

(b) Is strategy ALL B ("play B unconditionally in all iterations of the game") an WESS? (Circle one.) YES NO

(c) Is strategy RECIPROCATE ("play A in period 1 and then play what the other player played in the previous period") an WESS? (Circle one.) YES NO

Problem 12

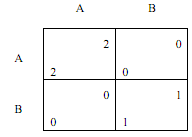
126_Games of repeated Prisoners Dilemma8.png

(a) Is strategy ALL A ("play A unconditionally in all iterations of the game") an WESS? (Circle one.) YES NO

(b) Is strategy ALL B ("play B unconditionally in all iterations of the game") an WESS? (Circle one.) YES NO

(c) Is strategy RECIPROCATE ("play A in period 1 and then play what the other player played in the previous period") an WESS? (Circle one.) YES NO

In the problems below assume that the evolutionary games involve an infinitely repeated Prisoner's Dilemma with one-shot payoffs of 0, 1, 3 and 5 and without discounting (payoffs are calculated as per-period average.)

Problem 13

Consider now the following strategies in an infinitely repeated Prisoner's Dilemma game: ALL D: defect unconditionally in all iterations of the game; STFT (suspicious tit for tat): defect in the first interaction and then cooperate if the other player cooperated on the previous interaction and defect if he defected; MACHO: defect in the first iteration; in second iteration cooperate if the other player defected in the first iteration and then play "tit for tat"; if he cooperated in the first iteration, defect unconditionally in all periods of the game from iteration 2 onwards; TF2T (tit for two tats): cooperate in periods 1 and 2. Thereafter defect in any period k>2 if and only if your opponent defected in k-1 and k-2.

Which strategies from the set above are weak ESS (WESS)? List all strategies that are weak WESS:

Problem 14

What is the relationship between Nash equilibrium and WESS? More specifically,

1. Can you find a strategy s such that (s, s) is in Nash equilibrium and s is not WESS? (Circle one.) YES NO

2. Can you find a strategy s which is WESS and (s, s) is not a Nash equilibrium? (Circle one.) YES NO

Problem 15

Can you find a strategy s such that u(s, s) = 3, (s, s) is in Nash equilibrium, and s is not WESS? Prove your claim.

Reference no: EM13815291

Questions Cloud

What is greed and is it greed good or bad : What is greed? Is it greed good or bad?
How america would be different if events had not occurred : During the Reagan / Bush years there were many changes in America. Pick two from the list and discuss how America would be different if these events or people had not occurred or existed, or had events happened differently.
Acc 304 prepare the lower portion of the income statement : The following are partial income statement account balances taken from the December 31, 2009, year-end trial balance of White and Sons, Inc. Restructuring costs 300,000 Interest revenue 40,000 Loss from earthquake (unusual and infrequent) 400,000 Los..
Case study on patricia and ira : Patricia and Ira
Nash equilibrium in the repeated prisoners dilemma game : Consider an infinitely repeated Prisoner's Dilemma game with values of δ sufficiently close to (but not equal to) 0. Which of the following are true - Nash equilibrium in the repeated Prisoner's Dilemma game without discounting
Case study on understanding sexuality : Normal 0 false false false EN-US X-NONE X-NONE Understanding Sexuality
Define parens patriae and due process : Define parens patriae and due process. What are the unintended consequences of providing youths with greater due process rights in juvenile court? How does the concept of parens patriae conflict with due process
Did jfk handle the cuban missile crisis correctly : Did JFK handle the Cuban Missile Crisis correctly? Did he nearly push the Soviets too far? Did his decisions show a penchant for living dangerously?

Reviews

Write a Review

Game Theory Questions & Answers

  Use the best-response approach to find all nash equilibria

Player 1 has the following set of strategies {A1;A2;A3;A4}; player 2’s set of strategies are {B1;B2;B3;B4}. Use the best-response approach to find all Nash equilibria.

  A supplier and a buyer, who are both risk neutral

A supplier and a buyer, who are both risk neutral, play the following game,  The buyer’s payoff is q^'-s^', and the supplier’s payoff is s^'-C(q^'), where C() is a strictly convex cost function with C(0)=C’(0)=0. These payoffs are commonly known.

  Pertaining to the matrix game theory problem

Pertaining to the matrix need simple and short answers, Find  (a) the strategies of the firm (b) where will the firm end up in the matrix equilibrium (c) whether the firm face the prisoner’s dilemma.

  Nash equilibria

Consider the two-period repeated game in which this stage game is played twice and the repeated-game payo s are simply the sum of the payo s in each of the two periods.

  Find the nash equilibrium

Two players, Ben and Diana, can choose strategy X or Y. If both Ben and Diana choose strategy X, every earns a payoff of $1000.

  Construct the payoff matrix for the game

The market for olive oil in new York City is controlled by 2-families, Sopranos and Contraltos. Both families will ruthlessly eliminate any other family that attempts to enter New York City olive oil market.

  Question about nash equilibrium

Following is a payoff matrix for Intel and AMD. In each cell, 1st number refers to AMD's profit, while second is Intel's.

  Finding the nash equilibrium

Determine the solution to the given advertising decision game between Coke and Pepsi, assuming the companies act independently.

  Nash equilibria to determine the best strategy

Little Kona is a small coffee corporation that is planning entering a market dominated through Big Brew. Each corporation's profit depends on whether Little Kona enters and whether Big Brew sets a high price or a low price.

  Creating a payoff table

Suppose you and your classmate are assigned a project on which you will earn one combined grade. You each wish to receive a good grade, but you also want to avoid hard work.

  Determine the nash equilibrium for trade policy

Consider trade relations in the United State and Mexico. Suppose that leaders of two countries believe the payoffs to alternative trade policies are as follows:

  Find the nash equilibrium outcomes

Use the given payoff matrix for a simultaneous move one shot game to answer the accompanying questions.

Free Assignment Quote

Assured A++ Grade

Get guaranteed satisfaction & time on delivery in every assignment order you paid with us! We ensure premium quality solution document along with free turntin report!

Submit Assignment

Academics

Major Subjects

Majors

Get In Touch

whatsapp: +1-415-670-9521

Phone: +1-415-670-9521

Email: [email protected]

TERMS & POLICIES

HELP & SUPPORT

All rights reserved! Copyrights ©2019-2020 ExpertsMind IT Educational Pvt Ltd