Reference no: EM13148802
The Multiple Linear Regression Model: Analysis
To begin, open the Gretl, go to file > open data > sample file, then open the data set under the "Ramanathan" tab labeled: "data 4-5 Women's labor force participation".
We will be conducting analysis on the determinants of the percentage of a state's labor force (16 years of age or older) who are female (hence, there are 50 observations for the 50 states in the U.S.). The determinants (i.e. the explanatory variables) are variables describing characteristics of the overall and the female population in the state with the expectation that at least some of these characteristics may explain the variation in female labor force participation witnessed across the 50 states in whatever year this data was collected.
So, wlfp will be our dependent variable and the remaining variables will be our explanatory variables in our full, unrestricted model.
a) First, you need to fully understand what we are modeling. So, write out the general, unrestricted, linear function which we will be estimating using OLS (the PRF). Below this, list the variables as they are labeled in the data and beside each variable label, in a complete sentence, describe each variable fully, paying attention to the units of the variables (Note: keep in mind that when we view the summary statistics of the percentage variables we can tell that any variable that is described as a "percent" are coded in terms of full percentage values, not decimals).
b) Estimate the linear model described in part (a) using Ordinary Least Squares regression and display your regression results. Briefly, mention which estimated coefficients are statistically significant (different than zero) and at what level of significance (i.e., 1%, 5%, or 10%) (You do not need to implement a t test for each one). Also, report the Adjusted R-squared and interpret its meaning.
c) Interpret, fully, the estimated marginal effect (regression coefficient) of educ. Then, at the 5% level of significance, test the hypothesis that a five percent increase in the percent of the state population with a high school degree will increase women's labor force participation by more than one percent.
d) Interpret, fully, the estimated marginal effect (regression coefficient) of the unemployment rate on female labor force participation. Then, at the 5% level of significance, test the hypothesis that for every ½ of a percent increase in the unemployment rate a state's female labor force participation rate will decrease by 0.25%.
e) Use the reported F(8,41) statistic to test for the overall significance of our model at the 5% level of significance. Be sure to state the null and alternative hypotheses, the critical value, and your conclusion.
f) Test whether excluding variables for the female marriage and divorce rates will significantly decrease the explanatory power of our model at the 10% level of significance. (Hint: pages 116 - 117 of your textbook).
g) Using our full, unrestricted model, test whether the marginal effect (regression coefficient) of the percent of the state's population living in an urban area and the marginal effect (regression coefficient) of the percent of the state's population whose race is reported as white are equal.
Our hypothesis can be stated in the following manner,
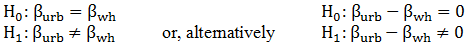
There are two ways to test such a constraint, the t-test is one; I'll help you get started:
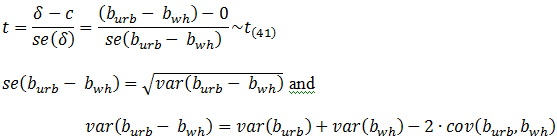
After estimating a model in Gretl you may view the variance-covariance matrix of the coefficients by clicking Analysis > Coefficient covariance matrix on the regression output screen. Each "cell" of this table is the covariance between the regression coefficients for the variables in the corresponding row and column of the table.
h) Finally, report the predicted female labor force participation rate in an average state.