Reference no: EM131003974

1. An office supply catalogue gives a description of bookshelves that includes the following variables. Which of these variables is qualitative?

A. The width of a bookshelf.
B. The price of a bookshelf.
C. The height of a bookshelf.
D. The colour of a bookshelf.
E. The depth of a bookshelf.

Use the information following to answer questions 2. and 3.

A sample was taken of the salaries of 14 randomly selected employees of a large company. The following are the salaries (in thousands of dollars) for this year.

60 35 42 47 75 37 61 32 49 67 54 42 53 42

2. Which of the following statements about the descriptive statistics (given in thousands of dollars) for these data are correct?

A. The mean = 49.7 and the standard deviation = 12.2
B. The range = 43 and the mean = 49.7
C. The mean = 48 and the mode = 42
D. The range = 43 and the standard deviation = 12.2
E. There is no mode and the standard deviation = 12.6

3. The interquartile range for the salaries (in thousands of dollars) for this year is

A. 7
B. 17
C. 25
D. 17.5
E. 18

4. When analysing quantitative data, the following graphical device is not appropriate:

A. Stem and leaf display
B. Histogram
C. Boxplot
D. Pie chart
E. Ogive

5. If the mean of a distribution is 5, the median is 6 and the mode is 7, then the distribution is:

A. negatively skewed.
B. symmetric.
C. bimodal.
D. positively skewed.
E. uniform.

6. The following marks are obtained by 5 students on a test:

8 16 24 4 13

The lecturer calculates the median to be 13. The lecturer however, then discovers that an error was made when recording the marks. The mark of 24 is actually a mark of 17. The new median would be:

A. 6
B. 13
C. 17
D. 10.5
E. None of the above.

Use the information following to answer questions 7. and 8.

A sample of 400 university academics was taken. Each academic was asked their age, sex, rank, annual salary, faculty and how many years they have been an academic. The following pie chart provides information about the ranks of the 400 academics sampled.

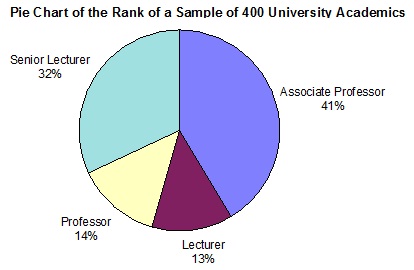
7. Based on the pie chart above, we may conclude that

A. Associate Professors have the highest annual incomes.
B. less than half of the academics sampled are Professors or Associate Professors.
C. Lecturers have the lowest annual incomes.
D. less than a quarter of the academics sampled are Professors.
E. Senior Lecturers earn more than Lecturers.

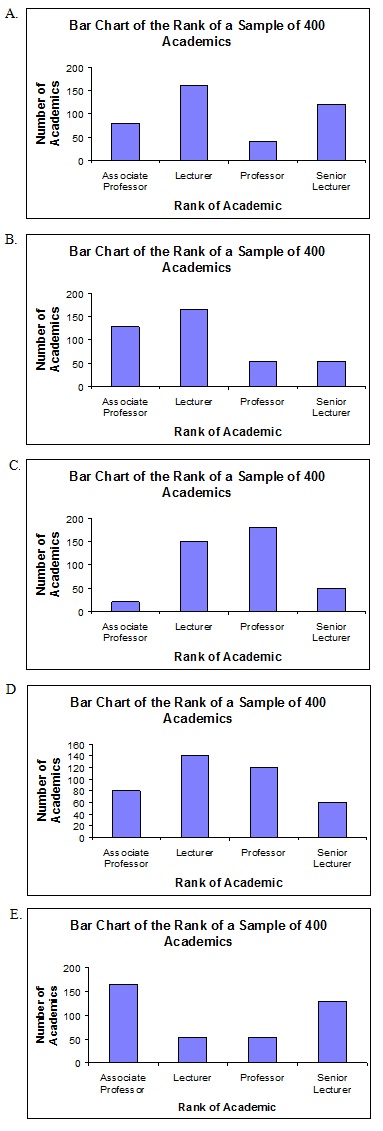
8. Which of the following bar graphs presents the same information as the pie chart?

9. The management of Disney world is interested in the time that people have to wait for a monorail. The following boxplot shows the distribution of the waiting times.

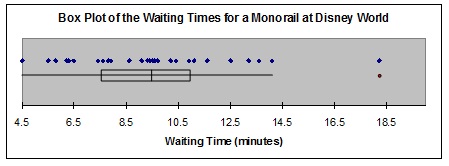
Choose the statement which most correctly describes the distribution of the waiting times for a monorail at Disney World.

A. The mean waiting time was 9.45 minutes.
B. No-one had to wait more than 15 minutes.
C. 50% of people waited more than 9.45 minutes.
D. More than 75% of people waited more than 10.95 minutes.
E. 25% of people waited between 7.55 and 10.95 minutes.

10. A marketing consultant observed 50 shoppers at a supermarket. One variable of interest was how much each shopper spent in the store. The amounts (in dollars) spent in the store by the 50 shoppers were organised into the following frequency distribution using Excel.

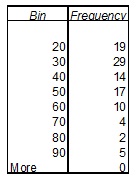
The Excel histogram which most correctly represents the data is given by

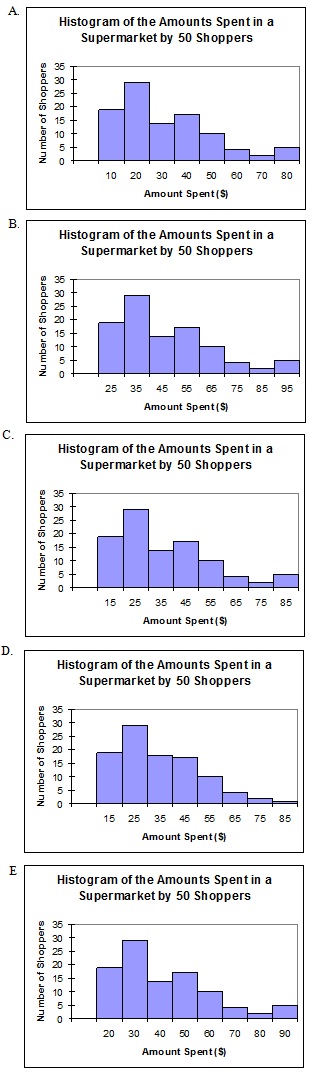
11. A box of marbles contains 3 white marbles, 4 black marbles, and 1 blue marble. If two marbles are selected at random, what is the probability of selecting 1 white marble and 1 blue marble (without replacement)?

A. (3/8) x (1/7)
B. (3/8) x (1/7) + (1/8) x (3/7)
C. (3/8) x (1/8) + (1/8) x (3/8)
D. (3/8) x (1/8)
E. Can't be done, as there is only one blue marble.

Use the following information to answer questions 12. and 13.

It is estimated that the probability that a student will pass a subject is 0.8 and we assume that whether a student passes the subject or not is independent of whether other students pass the subject. In a class of 15 students,

12. Find the probability that exactly 12 will pass the subject.

A. 0.250
B. 0.602
C. 0.352
D. 0.750
E. none of the above.

13. Find the probability that at least 10 will pass the subject

A. 0.164
B. 0.061
C. 0.939
D. 0.836
E. 0.188

14. A shipping company can unload 8 ships per week and the average number of ships arriving each week is 6. If the total number of ships arriving per week is 8 or less the shipping manager does not have to pay overtime, if the number exceeds this the manager has to pay overtime, so that there is not a backlog for next week. Assuming the ships arrive randomly and independently. Find the probability that the manager will have to pay overtime for the week.

A. 0.084
B. 0.847
C. 0.916
D. 0.153
E. 0.069

15. A football team plays 55% of their games at home and 45% of their games away. Given that the team has a home game, there is a 80% chance they will win. Given that it is an away game, there is a 65% chance that they will win. If the team wins what is the probability that they played at home.

A. 55%
B. 80%
C. 65%
D. 44%
E. 60%

16. If P(A/B) = 0.8, P(A) = 0.5 and P(B) = 0.4 , then the P(A or B) is:

A. 0.32
B. 0.58
C. 0.90
D. 0.40
E. 0.70

17. Given that z is the standard normal variable, find P(0.6 < z < 2.6)

A. 2
B. 0.2257
C. 0.7210
D. 0.2696
E. 0.4953

18. Given that z is the standard normal variable, find α if P(z > α) = 0.8599

A. 1.08
B. -1.08
C. 0.36
D. -0.36
E. 0.3599

19. If X  is normally distributed with mean μ = 5, and standard deviation σ = 2, then P(2 < X < 8) is

A. 0.8664
B. 0.4332
C. 0.0668
D. 0.1336
E. 0.6332

20. A sample of size 16 is drawn from a population which is normally distributed with a mean of 20 and a standard deviation of 8. What is the probability that the sample will have a mean greater than 22.

A. 0.0987
B. 0.1587
C. 0.3413
D. 0.4013
E. 0.6587