Multiple choice test from spring 2002

Reference no: EM131004014

Use the following information to answer questions 1. through 4.

The number of small electric motors which were rejected due to for poor quality, per batch of 250, were recorded for recent batches. The results were as follows:

3 2 7 5 1 3 1 7 0 6 2

3 4 1 2 25 2 4 5 0 5 3

5 3 1 2 3 1 3 0 1 6 3

5 41 1 0 6 4 1 3

1. If we treat these data as a sample, the mean and standard deviation number of rejects are

A. 3 and 7.1 respectively.
B. 4.4 and 7.0 respectively.
C. 4.5 and 7.1 respectively.
D. 4.4 and 50.1 respectively.
E. 4.4 and 7.1 respectively.

2. The median and modal number of defects is

A. 3 and the data set is bimodal with modes of both 1 and 3.
B. 3 and 3 respectively.
C. 3.5 and 3 respectively.
D. 3.5 and the data set is bimodal with modes of both 1 and 3.
E. 5 and 3 respectively.

3. We want to use Excel to generate a frequency distribution and histogram for these data. The most appropriate bin values for generating these would be

A. 0 6 12 18 24 30 36
B. 5 10 15 20 25 30 35 40 45
C. 7 14 21 28 35 42
D. 5 11 17 23 29 35 41
E. 10 20 30 40 50

4. Following is a boxplot showing the distribution of the number of rejected motors.

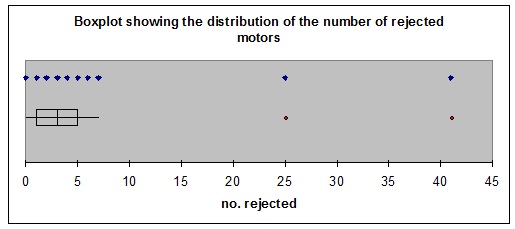
1560_Boxplot-number of rejected motors.jpg

Choose that statement which most correctly describes the data in the boxplot.

A. There are no outliers in the data set.
B. The data are positively skewed.
C. The data are approximately symmetric.
D. The data are negatively skewed.
E. 50 % of the data lie between 3 and 7.

5. The annual income for 200 recently graduated business graduates is summarised in the frequency distribution which follows.

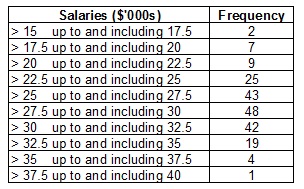
433_Annual income-frequency distribution.jpg

The mean and standard deviation salary would be

A. approximately $27.98 and $4.11 respectively.
B. approximately $27.98 and $4.10 respectively.
C. exactly $27 975 and $4 106 respectively.
D. approximately $27 975 and $4 106 respectively.
E. exactly $27 975 and $4 096 respectively.

6. Following is an ogive showing the time in days to complete the year-end audit for a sample of 20 customers from a large public accounting firm.

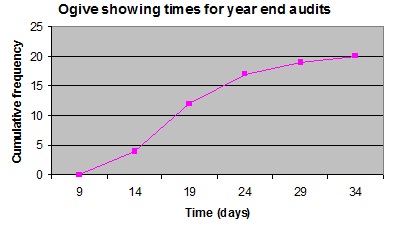
2316_Ogive-times for year end audits.jpg

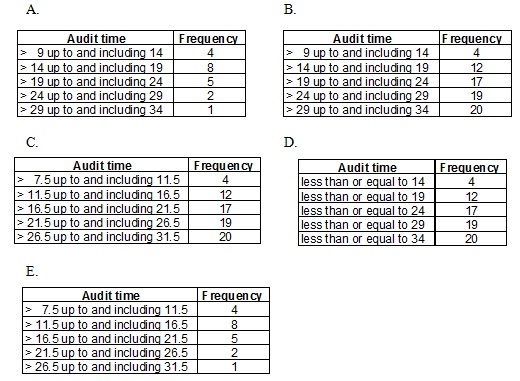
Select the frequency distribution, which accurately represents the data in this ogive.

824_Data in ogive.jpg

7. A management consultant conducts seminars for individuals who are interested in starting a new business. Each seminar is limited to six participants who, because of the nature of the seminars, often become clients for the management consultant. Based on the long-term experience of the management consultant, the probability distribution for x, the number of participants from each seminar who become clients is given in the following table.

X 0 1 2 3 4 5 6
ρ(X) 0.05 0.10 0.20 0.25 0.15 0.15 0.10

The expected value and variance of this distribution would be

A. E(X) = 3 and V(X) = 2.7
B. E(X) = 3.2 and V(X) = 12.9
C. E(X) = 3.2 and V(X) = 3.6
D. E(X) = 3.2 and V(X) = 2.7
E. E(X) = 3.2 and V(X) = 1.6

8. If P(A) = 0.3, P(B) = 0.6, and P(A|B) = 0.2, then P(A and B) is

A. 0.06
B. 0.90
C. 0.12
D. 0.18
E. 0.33

9. Data relating to the years of experience for employees of a large accountancy firm would be classified as

A. qualitative and nominal.
B. quantitative and ordinal.
C. qualitative and ratio.
D. quantitative and interval.
E. quantitative and ratio.

Use the information following to answer questions 10. and 11.

A study concerning the relative influence of husbands and wives in consumer purchasing, reported that the husband exerts the primary influence in selecting the make of a new car in about 70% of all new-car purchases by families. Suppose 10 families have decided to buy a new car.

10. What is the probability that in exactly eight of the ten families, the husband will exert the primary influence in choosing the make of car?

A. 0.058
B. 0.148
C. 0.851
D. 0.234
E. 0.617

11. What is the probability that the husband will exert the primary influence in choosing the make of car in more than half of the ten families?

A. 0.103
B. 0.200
C. 0.150
D. 0.850
E. 0.953

12. On average, five people per day enter the intensive care unit of a local hospital on any given day. If the people arrive randomly and independently, what is the probability that the number of people entering the intensive care unit on a particular day is between six and ten?

A. 0.206
B. 0.233
C. 0.352
D. 0.379
E. 0.794

13. If Z is the standard normal random variable, then P(Z < 1.07) is

A. 0.1423
B. 0.6423
C. 0.9554
D. 0.8577
E. 0.3577

14. If Z is the standard normal random variable, then P(-2.43 ≤ Z ≤ -1.5) is

A. 0.1394
B. 0.9257
C. 0.0593
D. 0.9407
E. 0.0793

Use the following information to answer questions 15. and 16.

From past experience, the management of a well known fast food restaurant estimates that the number of weekly customers at a particular location is normally distributed, with a mean of 5000 and a standard deviation of 500 customers.

15. What is the probability that on a given week the number of customers exceeds 6500?

A. 0.4987
B. 0.9987
C. 0.0013
D. 0.0010
E. 0.4990

16. For 95% of the weeks, the number of customers should exceed what amount?

A. 4525
B. 4975
C. 5472
D. 4177.5
E. 5822.5

17. The average weekly expenditure on entertainment for a population in a given region is $19.50, and the population standard deviation is $5.30. What is the probability that a random sample of 100 will yield a sample mean greater than $20.00?

A. 0.1736
B. 0.3264
C. 0.8264
D. 0.0359
E. 0.4641

Use the following information for questions 18. and 19.

A sample of 100 chocolate bars selected was found to have a mean weight of 99.5gm with a standard deviation of 2gm.

18. The 95 % confidence interval estimate of the true mean weight of all chocolate bars produced would be calculated by

A. 99.5 ± (1.96)(0.2)
B. 99.5 ± (1.96)(0.02)
C. 99.5 ± (1.984)(0.2)
D. 99.5 ± (1.984)(0.02)
E. 99.5 ± (1.660)(0.2)

19. What size sample would have to be taken in order to estimate the true mean weight of chocolate bars to within 0.2gm with 90% confidence?

A. 165
B. 164
C. 1083
D. 1082
E. 271

20. A firm's management is contemplating modifying one of its products. To help in making the decision, management representatives plan to conduct a market survey that will enable them to estimate the proportion of potential customers who would buy the new modified product. From a random sample of 100 customers selected, 40 indicated that they would buy the new modified product. The 99% confidence interval for the true proportion of all customers who would buy the new modified product would be calculated by

A. 40 ± (2.575) √[(0.4)(0.6)/100]
B. 0.4 ± (2.575) √[(0.4)(0.6)/100]
C. 0.4 ± (2.326) √[(0.4)(0.6)/100]
D. 0.4 ± (2.626) √[(0.4)(0.6)/100]
E. unable to be determined since are not both greater than 5.

Reference no: EM131004014

Questions Cloud

General overview of the plan you choose : In a 2-3 page paper, give a general overview of the plan you choose for this assignment. Consider each of the 10 components and describe how the company has included this component

What is the value of net domestic product : Given the following annual information about a hypothetical country, answer questions a through d. What is the value of GDP? What is the value of net domestic product?

Summarizing the meeting and discussing important concepts : Write a two-part paper of 750-1,000 words summarizing the meeting and discussing important concepts presented in the meeting

Show that the unit binormal vector makes a constant angle : Consider the helix with arc-length parametrization r(s) = αcos(αs)i + αsin(αs)j + αbsk, α - (a2 + b2)-1/2. Show that the unit binormal vector makes a constant angle with the axis of the cylinder on which the helix lies.

Multiple choice test from spring 2002 : The annual income for 200 recently graduated business graduates is summarised in the frequency distribution which follows.

What is gross about gross domestic product : (Consumer Price Index) One form of the CPI that has been advocated by lobbying groups is a "CPI for the elderly." The Bureau of Labor Statistics currently produces onlyindexes for "all urban households" and "urban wage earn- ers and clerical worke..

What are the instructional implications of learning styles : What are the instructional implications of learning styles and what are the research difficulties? What do you think is your learning style

Find the resolution of an analogue-to-digital converter : Find the change in resistance of an electrical resistance strain gauge with a gauge factor of 2.0 and a resistance of 100 Ω when subject to a strain of 0.001.

Advance collection for magazine subscriptions : Identify the accounting principle(s) applicable to each of the following situations: a. Tim Roberts owns a bar and a rental apartment and operates a consulting service. He has separate financial statements for each. b. An advance collection for mag..

User Account

All Pages