MTH103 Introduction to Applied Mathematics Assignment

Reference no: EM132527989

MTH103 Introduction to Applied Mathematics - University of the Sunshine Coast

Problem 1.

(a) A series of measurements were made during an experiment to calculate the total energy of a system. The values m = 15.5, h = 1.22 and v = 2.50 combined with g = 9.81 (all in their SI units) are needed for the formula

E = mgh + 1/2 mv². By entering your calculations directly into the table below, use your knowledge of significant figures to calculate the reported value of the total energy E.

(b) The efficiency H of a computer compilation is given by H = 1/q + p(1-q) where p is the number of computer processors. Find p for H = 0.66 and q = 0.83.

(c) Using a drone, the widths of an area burned by a bush fire were measured at 500m intervals, as shown in the following table. Determine the approximate area burned by the bushfire using Simpson's Rule.

Distance (km)	0.000	0.500	1.000	1.500	2.000	2.500	3.000	4.000	4.500
Width (km)	1.330	2.243	4.507	6.200	2.595	0.665	2.843	1.512	0.406

Problem 2.

(a) Triangle ABC has side a = 74.8, side b = 87.5 and angle C = 62.0°. Solve for the third side c and the other two angles.

(b) Scientists can use a set of footprints to calculate an animal's step angle, which is a measure of walking efficiency. In the photograph, it is angle ABC. The closer the angle is to 180 degrees, the more efficiently the animal walked. For the set of footprints shown, AC = 104cm, BC = 67cm and AB = 65cm. Find the step angle.

Problem 3.

(a) Find the vector cross product for 3D vectors a and b when

a = 2i - j + k and b = i + j.

(b) Find the magnitude and direction of the resultant force for the three forces shown in the diagram.

Problem 4.

(a) Which of the following is the greater angle measure: 150.0° or 2.540 radians?

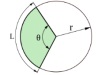
(b) Calculate the arc length L and the area of the sector when θ = 2.21 radians and r = 2.10m.

(d) Solve the following system of equations using a matrix method:

x + ?? + z = 4, 3x + 3?? = 12, 2x - 5z = 4.

Problem 5.

(a) Steam in a boiler was heated to 150? and then allowed to cool. Its temperature ?? was recorded each minute as shown in the following table:

Time (min)	0.00	1.00	2.00	3.00	4.00	5.00
Temperature (?)	150.0	142.8	138.5	135.2	132.7	130.8

Use linear interpolation to estimate the approximate temperature at 1 minute and 15 seconds.

(b) Solve the following equations for the unknown variable:

(i) (x-1)/2x = 0.25

(ii) cos x = -0.866025 (180° ≤ x ≤ 270°),
(iii) ln c^4.5 = 10.5 (to 2 decimal places)
(iv) e^4x+1 = 10x (to 4 decimal places).

Reference no: EM132527989

Questions Cloud

What is learned from the psychology course : What is learned from the psychology course as a whole. This is a position paper A position paper is your synthesis of ideas and thoughts regarding psychology

Create alpha company general journal entries to record : Create Alpha Company's general journal entries to record the purchase and payment for inventory purchased from its Japanese vendor?

The measurement of central tendencies : The Measurement of Central Tendencies The central measure of tendencies for the data sets of years of school completed and mother's education

Prepare the january and november general journal entry : How would you use this information to prepare the January 1, November 15 and December 31, 2017 General Journal entry (without explanation)?

MTH103 Introduction to Applied Mathematics Assignment : MTH103 Introduction to Applied Mathematics Assignment Help and Solution, University of the Sunshine Coast - Assessment Writing Service

Prepare the adjusting general journal entry for the december : How would you use this information to prepare the adjusting General Journal entry (without explanation) for the December 31, 2017?

How you met the essential by referring to the assignments : Identify how you met the essential by referring to the assignment(s) specifically in your response. Additionally, reflect on and make connections between your.

How accounting information systems assists in business : Discuss how Accounting Information Systems (AIS) assists in business integration with external parties such as suppliers and customers.

Describe the intervention or treatment tool in brief : As a group, identify a research or evidence-based article published within the last 5 years that focuses comprehensively on a specific intervention or new.

User Account

All Pages