Reference no: EM132808369
MST210 Mathematical methods, models and modelling - The Open University
Question 1
This question (and the next) start the assessment of the modelling strand of MST210. The aim of the modelling strand is to complete the modelling activity and write a modelling report, which is submitted as TMA 07. The questions here are designed to help you to write your modelling report by examining what makes a good report. To help you in this task of critically evaluating modelling reports, you are asked to assume the role of a tutor awarding marks.
Appendix 1 describes a modelling problem that is similar to the problem that you will consider for the modelling activity. Appendices 2 and 3 contain modelling reports that address this problem. Appendix 4 contains tutor notes for marking the modelling reports (this is an excerpt from the tutor notes for TMA 07).
(a) Award a mark (out of 5) for the Specify the purpose section of the report in Appendix 2. Write a brief statement to justify the amount of marks you award in a style suitable for feedback to an MST210 student.
(b) Award a mark (out of 30) for the Create the model section of the report in Appendix 2. Write a brief statement to justify the amount of marks you award in a style suitable for feedback to an MST210 student.
(c) Award a mark (out of 10) for the Do the mathematics section of the report in Appendix 2. Write a brief statement to justify the amount of
marks you award in a style suitable for feedback to an MST210 student.
(d) Award a mark (out of 10) for the Interpret the results section of the report in Appendix 2. Write a brief statement to justify the amount of marks you award in a style suitable for feedback to an MST210 student.
Question 2
Your task in this question is the same as the previous question, but you are now asked to consider the second modelling report contained in Appendix 3. (a)Award a mark (out of 5) for the Specify the purpose section of the report in Appendix 3. Write a brief statement to justify the amount of marks you award in a style suitable for feedback to an MST210 student.
(b) Award a mark (out of 30) for the Create the model section of the report in Appendix 3. Write a brief statement to justify the amount of
marks you award in a style suitable for feedback to an MST210 student.
(c) Award a mark (out of 10) for the Do the mathematics section of the report in Appendix 3. Write a brief statement to justify the amount of marks you award in a style suitable for feedback to an MST210 student.
(d) Award a mark (out of 10) for the Interpret the results section of the report in Appendix 3. Write a brief statement to justify the amount of marks you award in a style suitable for feedback to an MST210 student.
Question 3
A particle P of mass 2m is attached to a model spring of natural length l0 and stiffness k. The other end A of the spring is attached to a fixed point, and the spring hangs vertically downwards. A second spring of natural length l0 and stiffness 2k is attached to the particle, with its other end being fixed at the point B at a vertical distance 4l0 below A, as shown in the diagram below.
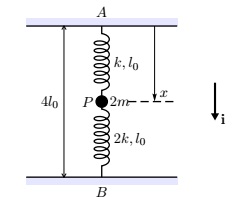
The particle is displaced vertically and then released so that the system oscillates in one dimension. You may ignore air resistance in this question. Take the origin at A and the x-axis in the direction from A to B, as shown in the diagram.
(a) Draw a force diagram indicating all the forces acting on the particle, and briefly describe each force.
(b) Copy and complete the following table to give the force due to each spring. The notation is the same as that used in the unit.
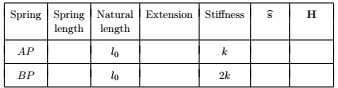
Express all the other forces in component form.
(c) Derive a differential equation of motion for the particle.
(d) Find the equilibrium position of the particle.
(e) Write down the general solution of the differential equation that you obtained in part (c).
(f) Hence write down the period of the oscillations of the particle when it is in motion, in terms of the given parameters.
Question 4
This question concerns a system with potential energy function given by
U (x) = -2x4 - x3 + 11x2 + 4x - 8 (-∞ < x < ∞),
whose graph is sketched below.
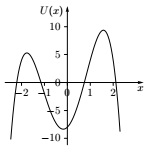
(a) Suppose that the total energy of the system is a constant, E = 2. Using Maxima, or otherwise, find the range or ranges of x-values (accurate to one decimal place) that could represent a motion of the system. Justify your answer by including an appropriate graph, or Maxima printout (such as your input to and the Maxima output from the command find_root or the command allroots), or details of your calculation.
(b) Now suppose that the total energy is E = 10. Find the range or ranges of x-values (accurate to one decimal place) that could represent a motion of the system in this case.
Question 5
The suspension of a modified baby bouncer is modelled by a model spring AP with stiffness k1 and a model damper BP with damping coefficient r. The seat is tethered to the ground, and this tether is modelled by a second model spring CP with stiffness k2. Model the combination of baby and seat as a particle of mass m at a point P that is a distance x above floor level. The bouncer is suspended from a fixed support at a height h above the floor. The suspending spring has natural length l1, while the tethering spring has natural length l2. Take the origin at floor level, with the unit vector i pointing upwards, as shown in the following diagram.
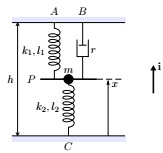
(a) Draw a force diagram showing all forces acting on the particle P.
(b) Copy and complete the following table, and hence write down the force on particle P due to each model spring. The notation is the same as that used in the unit.
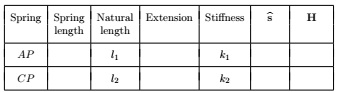
(c) Copy and complete the following table, and hence write down the force on particle P due to the model damper. The notation is the same as that used in the unit.

(d) Model the remaining forces acting on the particle that the equation of motion of the mass is P , and hence show
mx¨ + rx? + (k1 + k2)x = k1(h - l1) + k2l2 - mg. [4]
(e) In SI units, suppose that m = 9, k1 = 74, k2 = 70, r = 36, h = 2, l1 = 0.75 and l2 = 0.75. Determine the natural angular frequency of the system to two decimal places.
Using the same data, calculate the damping ratio for this mechanical system to two decimal places, and hence state whether the system undergoes strong, weak or critical damping. Comment on whether this damping is appropriate for a baby bouncer.
Question 6
Consider a particle that moves according to the equation of motion 10x¨ + 20x? + 160x = 20 cos(?t),
where ? is a constant.
(a) Suppose that ? = 3. Calculate the amplitude of the resulting oscillations of the particle after a long time has elapsed.
(b)Calculate the damping ratio for this mechanical system to two decimal places, and hence state whether the particle can undergo resonance.
Question 7
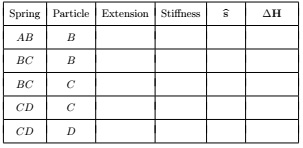
Three particles, B, C and D, of masses m, m/2 and m, respectively, are connected to three springs as shown in the following diagram.

The left-hand spring is connected to a fixed point A, and the particles are constrained to move in a straight line on a smooth horizontal surface. Each spring has natural length l0. Spring AB has stiffness 2k, spring BC has stiffness 3k, and spring CD has stiffness k. The particles are displaced from their equilibrium positions and released. The displacements of the particles B, C and D from their equilibrium positions are x1, x2 and x3, respectively, and time t is measured from the instant when the particles are released.
(a)Draw a force diagram showing all the forces acting on each particle.
(b)Copy and complete the following table to give the change in spring force from equilibrium for each spring acting on each particle. The notation is the same as that used in the unit.
(c)Hence derive the equation of motion for each particle, and show that in matrix form these equations may be expressed as
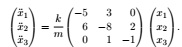
Question 8
The oscillations of three particles A, B and C are governed by the matrix equation

where x, y and z are the particles' respective displacements from equilibrium.
(a) Show that the vector (0 .29 -0.75 0.59)T is an approximate eigenvector of the dynamic matrix (to two significant figure accuracy) by calculating the corresponding eigenvalue.
(b) Calculate the corresponding normal mode angular frequency for the normal mode with the given normal mode eigenvector.
(c) Give an initial displacement vector that would lead to the normal mode motion corresponding to the given eigenvector.
(d) For this normal mode motion, state (with a reason) which of the particles are moving in phase.
Attachment:- Mathematical methods - models and modelling.rar