MECH0018 Stress Analysis Assignment

Assignment Help Mechanical Engineering

Reference no: EM132539404

MECH0018 Stress Analysis - Middle East College

Learning Outcome 1: Critically evaluate the implications of the theories of elastic and plastic fracture mechanics and apply these to simple problems.

Learning Outcome 2: Review the applications of the linear Theory of Elasticity, Theory of Plasticity and Fracture Mechanics to practical design problems and identify the limitations of these theories.

Assignment Objective

The main objective of this assignment is to develop the students' understanding of stress analysis, behavior of materials and finite element solution procedures, thus enabling them to select and apply concepts creatively in the solution to complex problems of stress analysis in design.

Problem 1:

(A) The ductile behaviour of a certain metal is well described by σ = 90000ε^0.25. The metal undergoes uniform work hardening process to a reduction in area of r = 40%, find the yield stress of the work-hardened metal.

(B) If the metal in (A) above, governed by the same ductile behavior equation, is cold-worked first by 30% which is still followed by an additional cold work of 35%, find the yield stress of the metal.

(D) If a bar of same metal of (A) above is initially cold worked some unknown amount. It is then subjected to 20% additional cold work and its yield strength is measured as 78,541 n/m². What was the unknown amount of cold work induced prior to the 20% added cold work?

Problem 2:

(A) A 65.4 mm wide aircraft inspection panel is made of 7074-T651 aluminium alloy. The material properties are (Fracture toughness, KIc = 25.8 MN m^-3/2 and Yield stress, σ_y = 505 MPa. Following inspection, an edge through-crack, a, of length 6.4 mm is found. During flight, this plate is subjected to a cyclic stress of 90 MPa. Ignoring the effect of the mean stress, calculate the number of cycles to failure (Nf) using Paris' Law and the material constants (in their standard units): A = 1.5x10^-12 m/(MNm^-3/2)n per cycle and m = 2.8, (Take Y = 1.12)

(B) Discuss the effect of the fracture toughness KIc if its value reduced to be 20 MN m^-3/2

Problem 3:

A 60 mm wide sample plate of 7074-T8 aluminium alloys is shown in Fig. 1 and it contains a central crack length, 2a, and fracture toughness, K_c = 22,200,000 Nm^-3/2 and the yield strength, σ_y = 520,000,000 N/m².

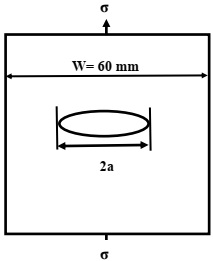
(A) If the applied stress, σ = 150,000,000 N/m², determine if the plate will fracture for a crack half-length of 6 mm, and 8 mm.

(B) Determine the critical half crack-length, ac, below which the plate will fail by yielding (Take Y = 1).

(C) Discuss the following categories of Stress-Strain Relationship in details:
- Perfectly elastic
- Elastic and perfectly plastic
- Elastic and strain hardening

Problem 4:

The vertical rectanguler cross section column shown in Fig. Q4 is pinned at both ends. Assuming the young's modulus E for the column material is 200 GPa, σ_y = 250 MPa, L = 4 m, a = 30 mm, and b = 50 mm:

A) Find the maximum compressive load P that can be applied to the column without failure

B) Determine the allowable load.

C) Do you think this column will yield before it buckled? (Take FS = 2.5)

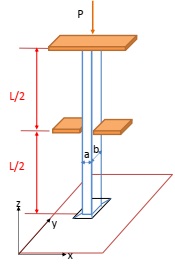
Fig. Q4: Rectangular Cross Section Column

D) What is the difference in the results of A, B, and C above if the column length is (L = 6 m)? Discuss the difference.

Attachment:- Stress Analysis.rar

Reference no: EM132539404

Questions Cloud

Staff member to help them get a changing room : You are a regional manager at the Walk-In Closet clothing store and you just received the most recent feedback from a mystery

What amount should be reported as amortization expense : On January 1, 2020, LMN Co. bought a trademark from PQR, Inc. for $500,000. What amount should be reported as amortization expense

How think today low interest rate environment is impacting : How do you think today's low interest rate environment is impacting the time value of money? How might this change the value of an asset or liability?

About the assorted reasons businesses diversify : About the assorted reasons businesses diversify. The reasons should include profit motive, tax reduction reasons, avoidance of anti-trust laws,

MECH0018 Stress Analysis Assignment : MECH0018 Stress Analysis Assignment Help and Solution, Middle East College - Assessment Writing Service - Critically evaluate the implications of the theories

Compute the depreciation for the first year : Compute the depreciation for the first year using the straight-line method of depreciating, the units of production method of depreciating

How should company f report the facts on the december : How should company F report the above facts on its December 31, 20XX balance sheet and income statement? Support your answer.

Aligned innovation guidelines are established : What might be some strategies executives could implement to help ensure effective and aligned innovation guidelines are established?

Understand disease trends in health care : As a health care manager, why is it important to understand disease trends in health care?

User Account

All Pages