Reference no: EM132527912

Unit 8 Mathematics for Construction - Applying principals of Mathematics in Sport Club Assessment

Learning Outcome 1 Identify the relevance of mathematical methods to a variety of conceptualized engineering examples.

Learning Outcome 2 Investigate applications of statistical techniques to interpret, organize and present data by using appropriate computer software packages.

Learning Outcome 3 Use analytical and computational methods for solving problems by relating sinusoidal wave and vector functions to their respective engineering applications.

Learning Outcome 4 Illustrate the wide-ranging uses of calculus within different engineering disciplines by solving problems of differential and integral calculus.

Assignment Brief

You are working as a civil engineer in a business and engineering consultancy company. An investor reaches your company requesting a design proposal for an international sport club. The investor doesn't know much information about the average member's fees in the area where the sport club is intended to be built. Therefore, he requested your company to give him an approximate estimation about the fees. As a part of the team who is working on the project, the project manager assigned you the following tasks:

Table 1: Number of members expected to join the sport club over the coming 3 years for the different ages and sex.

Assessment Task# 1: (members regression and cost analysis)

A- Your report should include data for the number of members expected to join the sport club by the end of the years 4, 5, and 15. plot the relationship between years and number of members joining the sport club, using the data in the table above.

B- State in your report what type of progression the members' data follows.

C- Include in your report the total number of members that the sport club will be accommodated in the 10th year.

D- The sport club should have maintenance after each 2,000 accumulated annual members joining the sport club. You have to define in your report after how many years the first, second and third maintenance procedure will take place.

E- Assume that the expected average cost per member per year is 200JOD, the expected overhead cost is 100K JOD per year and the expected cost of employee's salary and maintenance of sports equipment is 300K JOD per year.

Question 1. Use Table.1 to find the average cost/year for the first 3 years individually if no member left the sport club.

Question 2. Use the dimension analysis to find a function for the average of profit/year and ensure that the derived function you found is dimensionally consistent.

F- The project manager requests data to be provided by the statistic department about the average members' fee /year on the area where the sport club is intended to be built. The data provided by the statistical department is in the attached Excel file will be sent by email. The data is collected from 100 sport club. The members' fee /year is found to have a normal distribution probability function.

Question 1. Find the range, mean and standard deviation of the data. You may use a software package for this part. However, you must show the equations applicable for this problem.

Question 2. Draw a histogram of the data of bin width of 50 JOD. You may use a software package for this part.

Question 3. What is the probability that at a given sport club the fee will be between 1000 and 1400 JOD.

Question 4. Market statistics of the statistical department state that the average members' fee on that particular area is less than 1250 ± 155JOD (μ ± σ). Your team suspects this statistic is an underestimation and consequently commence they're on study by studying 100 Sport club and finding that μsample = 1250. Based on this information conduct a hypothesis test to determine whether the statistical department's statistic is an underestimate or not at a 0.05 level of significance.

G-The marketing department modelled the probability of the ability of the members to pay more than 1250 JOD/year with a binomial probability distribution, where the probability of paying more than 1250 JOD/year is p = 0.73. For a population of 1000 members, if you choose a sample of 30 members, address the following:

Question 1. What is the probability of having exactly 20 member that would pay more than 1250?

Question 2. What is the probability of having no member that would pay more than 1250?
H- Use your answers from previous parts to give the investor an estimation and recommendation about the associate members fees. Noting that the investor does not have a technical background about the statistical terms, so you have to clarify for him in simple words what each term means and indicates.

Assessment Task #2: (Design analysis)
Consider that the geometry of the arc for billboard for the sport club is following the hyperbolic equation: γ = 10-0.658 cosh(x-4.025). It is required to attach two torches for each direction for billboard. The purpose of the torch is to give a clear vision for the cars parking, thus it should not be hanged no more than 7m in height. Accordingly, you have to define in your report the rang of the value of x where the torch could be hanged without violating the maximum allowable height. The billboard width is 6.5m.

*If the design was changed for the billboard and the arc geometry function was changed to γ = 2.75*(sin(30x) + e^3.011x), redefine the range of x that was found in the first part.

Assessment Task#3: Analysing Vibration Response of the slab.

Using the figure #1 and figure #2 (all the figures will be sent by email), it is required to check the slab behaviour for the roof floor in the sport club under throwing the lifting and the movement of using the sports equipment, in order to accomplish that, a simulation was performed for the slab and the vibrations (displacements) with time were found to have the following relationship:

y1 = 0.08 sin (2.532 + 3.45 t) cm

In your report, you are expected to:

Question 1. Define the maximum amplitude, frequency and phase angle of the displacement function.

Question 2. You are expected to apply compound angle identities in order to separate the displacement function into a function in terms of sine and cosine.

It is considered that the movement of the water in the Olympiad swimming pool will create a vibration in the same direction of y1 of the following equation:

y2 = 5/8 sin(8.78t - 0.0475)cm

Question 3. You are expected to model the combination between the two sine waves and find the displacement at time t=2 s, using both analytical and graphical methods.

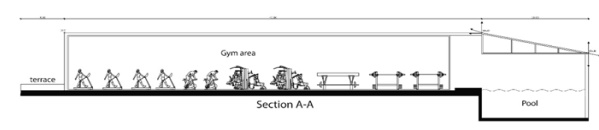
Figure #1: Section A-A of the sport club

Figure #2: Front view 3.D modelling of the sport club

Assessment Task#4: Checking the structural safety of the beams.

In order to check the overall structural safety for the skylight slab of the Olympiad swimming pool, you were requested to check the strength of the beams and this requires making analysis for the beams and finding the internal forces in each beam. Figure#1 and figure #3 show the skylight slab of the Olympiad swimming pool and the points where the beams are attached.

Figure #3: Side view 3.D modelling of the sport club

In your analysis report, you are expected to:

Question 1. Represent beam AB in vector form and find the length of the beam using the formula for the vector resultant.

Question 2. Represent the force in the beam in vector form, if each beam is carrying half the weight of the slab consider the weight is 6,000 kg, you have to find the force in each beam.