Reference no: EM132686071

Maximising the Volume of a Cake Tin

A cake tin manufacturer makes cake tins ranging in size from "tiny" to "gigantic". Some tins will be square based, others will be rectangular based, in all cases the manufacturer wants to maximise the volume of each cake tin.

Task

Investigate the size of a rectangle cut into a piece of tinplate to form an open top cake tin which optimises the volume. Through the use of mathematical calculations involving calculus some conjectures will be made.

Part 1 - Square Tinplate

An open top cake tin is to be made by cutting a square from each corner of a square piece of tinplate with side lengths 30 cm. Once the cut is made the sides are folded to form an open top cake tin. Let x cm be the side length of the square cuts to be made.

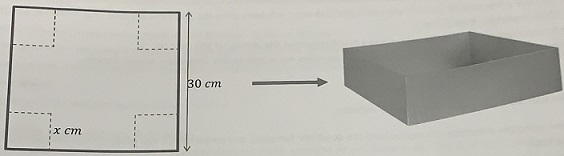
• Given the length of each side of the tinplate is 30cm, show that the volume of the cake tin can be expressed as V(x) = 900x - 120x² + 4x³ cm³
• Hence, use calculus techniques to find the exact value of x that will maximise the volume of the cake tin.
• Repeat the above process for at least two more square tinplates with side lengths other than 30cm
• Make a conjecture on what size squares should be cut from a square piece of tinplate with a side length 1 cm to maximise the volume of the cake tin.
• Prove your conjecture.
• Discuss any limitations and assumptions to your findings. (e.g. If you made a real cake tin, discuss any other factors that yot might need to consider.)

Part 2 - Rectangular Tinplate

Consider the following rectangular piece of tinplate with sides r cm and s cm. An open top cake tin is to be made by cutting a square (xcm by xcm) from each corner.

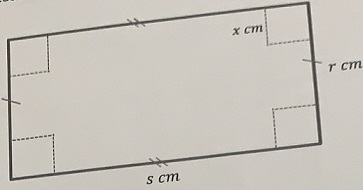
• Investigate the relationship between x (the cut to be made for the square) and the length of each side of the rectangle such that the cake tin has a maximum volume.
[hint: consider a few specific cases to start with and find exact solutions using the quadratic formula - e.g. a ratio of 1:2 for the sides of the rectangle, then 1:3 etc.]
• Make a conjecture on what values of r, s and x might maximise the volume of the cake tin.
• Summarise your findings and comment on any assumptions made and/or any limitations to your findings.
Possible extension work you might also consider includes:
• Prove, using the principles of calculus (and the quadratic formula), any conjecture(s) you proposed for the rectangular tin plate case.
• Investigate manufacturing different shapes of cake tin in order to minimise the cost of materials used. Compare the suitability and viability of producing them and suggest and discuss which shape of tin might be optimal.

Structure of a Mathematical Report

Introduction
This sectiovt describes what the ihvestigatioh will be about. It should include:
• any background (set the scene) information relevant to the main focus of the investigation
• the aim/purpose of the investigation (including the definition of any key terms (mathematical and non-mathematical) relevant to the corstext
of the problem)
• a description of how the investigation will be carried out
Mathematical Investigations & Analysis
This section colAtnivts all the data/jytfermatiort/colculations/results gathered or produced in the course of the isAvestigatior‘•
It includes:
• complete solutions to all set tasks set out in a clear and logical way
• appendices should only be used if there are extensive repetitive calculations and must be referenced appropriately)
• all results displayed appropriately and clearly (tables; graphs; diagrams)
• clear communication of all relevant information (including correct mathematical notation)
• interpretation and analysis of all results using complete sentences
• where applicable reference should be made to the reasonableness of the results (in terms of the context of the problem being investigate and any possible limitations of the interpreted results/original problem.
Conclusion
This sectiovt includes:
• a summary of all the main findings
• a clear statement of the overall conclusion(s)/solution (relating directly back to the aim)
• an evaluation of the results and methods used, including a comment on (where applicable)
o any assumptions made and any possible limitations of the interpreted results
o how the investigation could be extended to provide further results
o what worked well and what didn't (in terms of the process and calculations)
o any further investigations that could lead on from this one
Bibliography
• all sources used must be included and referenced appropriately.