Reference no: EM133104628

MATH136 Linear Algebra - University of Waterloo

Problems

Question 1: Let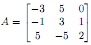. (In each part show your work.)
(a) Determine the characteristic polynomial of A. Express it in the form c₃λ³+ c₂λ²+ c₁λ+ c₀.

(b) Find all eigenvalues of A over R.
(c) Find all eigenvalues of A over C.
(d) Is A diagonalizable over R? Justify your answer.

(e) Is A diagonalizable over C? Justify your answer.

Question 2: Let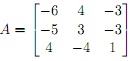. The eigenvalues of A are λ₁ = -2, λ₂ = -1 and λ₃ = 1. (In each part show your work. You may, however, omit row reduction details.)

(a) Explain why A is diagonalizable over R.

(b) For each of the eigenvalues, determine a spanning set for its corresponding eigenspace (over R). Each of your spanning sets must consist of exactly one vector.

(c) Determine an invertible matrix P and diagonal matrix D, both in M_3×3(R), such that P^-1AP = D. (You do not need to give P^-1.)

Question 3: (a) Let A ∈ M_n×n(F). Prove that if A is invertible and v^→ is an eigenvector of A, then v^→ is an eigenvector of A^-1. How are the corresponding eigenvalues related?

(b) Let A ∈ M_n×n(F). Let u^→ and v^→ be eigenvectors of A with eigenvalues λ₁ and λ₂, respectively. Prove that if λ₁ ≠ λ₂ then u^→ and v^{→ are not parallel.}

Question 4: Let A ∈ M_3×3(F). You are given the following information about A.

(i) A is not invertible.

(ii) The characteristic polynomial of A is of the form -λ³ + aλ + b for some a, b ∈ F.

(iii) A does not have three distinct eigenvalues in C.

Using this information, determine (with proof) the eigenvalues of A.

Question 5: Let A ∈ M_n×n(C). Prove that λ ∈ C is an eigenvalue of A² + I_n if and only if λ = µ² + 1 where µ ∈ C is an eigenvalue of A. [Hint: For the more difficult direction, consider the characteristic polynomial of A² + I.]