Solution-Math graph questions set, Correctly match each of

Math graph questions set

Assignment Help Mathematics

Reference no: EM1348318

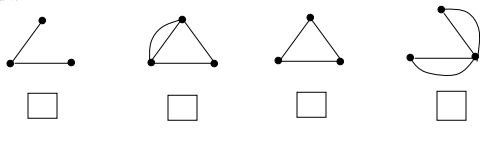
Question 1: Correctly match each of the following descriptions to a graph below by inserting the letter of the description that correctly describes the graph in the open box under the graph.

(A) The graph has both an Euler circuit and a Hamilton circuit.

(B) The graph has an Euler circuit but does not have a Hamilton circuit.

(D) The graph does not have an Euler circuit and does not have a Hamilton circuit.

Question 2. A graph G has a set of vertices V = {1, 2, 3, 4, 5, 6, 7} and a set of edges E = {(1,4), (1,5), (2,5), (2,6), (3,2), (3,4), (4,5) (4,6), (3,7), (5,7)}. Draw the graph G.

Question 3: Construct the incidence and adjacency matrices for each of the following graphs.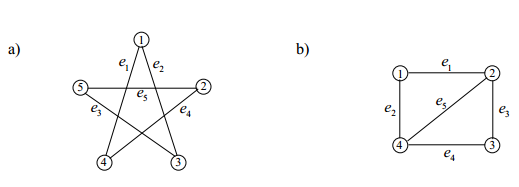

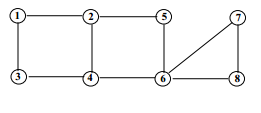
Question 4: Consider the adjoining connected graph consisting of 8 nodes and 10 edges.

Answer the following questions regarding this graph.

(a) Does this graph contain an Euler circuit? If your answer is yes, describe the circuit. If your answer is no, explain why there is no Euler circuit.

(b) Does this graph contain an Euler path? If your answer is yes, describe the path. If your answer is no, explain why there is no Euler path.

(c) Does this graph contain a Hamilton circuit? If your answer is yes, describe the circuit. If your answer is no, explain why there is no Hamilton circuit.

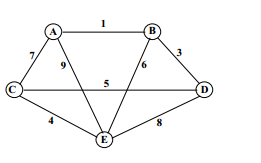
Question: 5. The adjoining diagram is a graph with five nodes (or vertices) labelled A, B, C, D and E. The lengths of the edges joining the nodes are shown on the graph.

a) Find all Hamilton paths going from node A to node B.

b) Find the lengths of each of the Hamilton paths from node A to node B.

Question 6. Consider the following digraphs. Draw their corresponding incidence matrices.

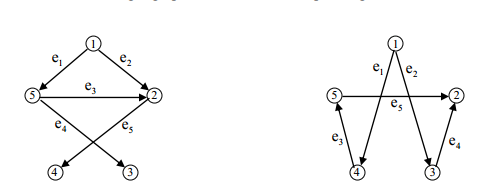
Question 7. Consider the following incidence matrix. Draw its corresponding digraph.

Question 8: Determine which two of the following three graphs A, B & C are equivalent

Question: 9. The adjoining graph consists of 6 nodes (or vertices) labeled A, B, C, D, E and F and 9 edges connecting pairs

of nodes. Does this graph contain an Euler path? If your answer is yes, provide an example of an Euler path for this graph. If your answer is no, explain why no Euler path exists.

Question 10. Give an example of a connected graph having the following properties. Note: The graph need not be a simple graph.

(a) A graph with 3 nodes that has both an Euler circuit and a Hamilton circuit.

(b) A graph with 4 nodes that has both an Euler circuit and a Hamilton circuit.

(d) A graph with 4 nodes that has an Euler circuit but not a Hamilton circuit.

Reference no: EM1348318

Questions Cloud

Explaining anticybersquatting consumer protection act : What does Anticybersquatting Consumer Protection Act perform? How does this act cut down on nuisance suits?

Calculate the cost of the preferred stock : Taylor Systems has just issued preferred stock. The stock has a 12% yearly dividend and a $100 par value and was sold at $97.50 each share. In addition, flotation costs of $2.50 each share must be paid.

Find the operating breakeven point : Given the values and cost data shown in the accompanying table for each of 3 firms, F, G, and H, answer the following questions.

Finding best companies to invest : Explain and discuss each corporation using fundamental analysis or technical analysis and select the best one (using current information).

Math graph questions set : Correctly match each of the following descriptions to a graph below by inserting the letter of the description that correctly describes the graph in the open box under the graph. The graph has both an Euler circuit and a Hamilton circuit.

Biologically inspired method : Biological ly Inspired Methods + Ma tlab Assignmen t, Define a problem of your choice which can be tackled by Biologically Inspired Methods. The problem must satisfy the following requirements

Statistical critical thinking and application skills : Statistical Critical Thinking and Application Skills, Discuss the research paper. Design and perform an experiment to answer the questions:

How you choose a research topic : In research, an epistemological stance will influence how you choose a research topic as well as the methodology and methods you use. Review the resources this week to explore the role of epistemology in research.

How does training employees contribute to overall success : How does training employees contribute to the overall success of the organisation? You are required to persuade the senior management team in your chosen organisation of the importance of employee development.

User Account

All Pages

Math graph questions set

Reference no: EM1348318

Reference no: EM1348318

Questions Cloud

Reviews

Write a Review

Mathematics Questions & Answers

Questions on ferris wheel

Logistic map

Finding the probability of cards

Systems of ode

Derive the boolean expression

System of equations

Linear programming problem

Find the natural domain

Introduction to numerical methods

Chart of the topological manifold

Mathematics in computing

Complex problems

Assured A++ Grade

Academics

Major Subjects

Majors

Get In Touch

TERMS & POLICIES

HELP & SUPPORT